
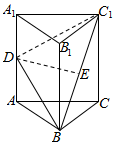
 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.分析 (1)取BC中点F,连结AF,EF,则可证四边形AFED是平行四边形,得出DE∥AF,将问题转化为证明AF⊥平面BB1C1C;
(2)过C作CM⊥BC1于M点,则CM⊥平面BC1D,于是∠CBC1就是BC与平面BC1D所成的角,在Rt△BCC1解出∠CBC1即可;
(3)V${\;}_{C-B{C}_{1}D}$=V${\;}_{D-BC{C}_{1}}$=$\frac{1}{3}{S}_{△BC{C}_{1}}•DE$.
解答 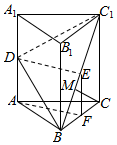 证明:(1)取BC中点F,连结AF,EF,
证明:(1)取BC中点F,连结AF,EF,
∵E,F分别是BC1,BC的中点,
∴$EF∥C{C_1},EF=\frac{1}{2}C{C_1}$,
∵$AD∥C{C_1},AD=\frac{1}{2}C{C_1}$,
∴EF∥AD,EF=AD,
∴四边形AFED为平行四边形,
∴DE∥AF,
∵△ABC为等边三角形,
∴AF⊥BC,
∵CC1⊥平面ABC,AF?平面ABC,
∴CC1⊥AF,又CC1?平面BB1C1C,BC?平面BB1C1C,BC∩CC1=C,
∴AF⊥平面BB1C1C,又DE∥AF,
∴DE⊥平面BB1C1C.
(2)由(1)可得,平面AFED⊥平面BB1C1C,
过C作CM⊥BC1于M点,则CM⊥平面BC1D,
∴∠CBC1就是BC与平面BC1D所成的角,
∵$tan∠CB{C_1}=\frac{{C{C_1}}}{BC}=\sqrt{3}$,
∴∠CBC1=60°.即BC与平面BC1D所成角为60°.
(3)∵△ABC是边长为2的等边三角形,∴AF=$\sqrt{3}$.∴DE=$\sqrt{3}$.
∴V${\;}_{C-B{C}_{1}D}$=V${\;}_{D-BC{C}_{1}}$=$\frac{1}{3}{S}_{△BC{C}_{1}}•DE$=$\frac{1}{3}×\frac{1}{2}×2×2\sqrt{3}×\sqrt{3}$=2.
点评 本题考查了线面垂直的判定,线面角的计算,棱锥的体积,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1007$\sqrt{2}$,1007$\sqrt{2}$) | B. | (-1007$\sqrt{2}$,1007$\sqrt{2}$) | C. | (1007,1007$\sqrt{3}$) | D. | (1007$\sqrt{3}$,1007) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
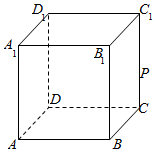 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
| 一年中出险的次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 频数 | 500 | 380 | 100 | 15 | 4 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
| 质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天数K | 5 | 23 | 22 | 25 | 15 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| x | 0 | 1 | 2 | 3 | 4 |
| y | 1 | 1.3 | 3.2 | 5.6 | 8.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com