
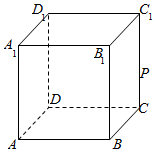
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.分析 解法一:(1)如图:连AC,设AC∩BD=O,$AP与面BDD_1^{\;}B_1^{\;}交于点G,连OG$.利用线面平行的性质可得:OG∥PC.利用三角形中位线定理及其线面垂直的判定可得:AO⊥平面BDD1B1,可得线面角,利用直角三角形的边角关系即可得出.
(Ⅱ)依题意,要在A1C1上找一点Q,使得D1Q⊥AP.只需D1Q⊥平面ACC1A1,设A1C1∩B1D1=O1,可推测A1C1的中点$O_1^{\;}$即为所求的Q点再利用线面垂直的判定与性质定理即可.
解法二:(1)建立如图所示的空间直角坐标系,利用法向量的性质、线面垂直的判定与性质定理、向量夹角公式即可得出.
(2)若在$A_1^{\;}C_1^{\;}$上存在这样的点Q,设此点的横坐标为x,依题意,对任意的m要使D1Q⊥AP,利用$\overrightarrow{{D}_{1}Q}$$•\overrightarrow{AP}$=0,解出x即可得出.
解答 解法一:(1)如图:连AC,设AC∩BD=O,$AP与面BDD_1^{\;}B_1^{\;}交于点G,连OG$.…(1分)$因为PC∥面BDD_1^{\;}B_1^{\;},面BDD_1^{\;}B_1^{\;}∩面APC=OG$,
故OG∥PC.所以$OG=\frac{1}{2}PC=\frac{m}{2}$.
又$AO⊥DB,AO⊥BB_1^{\;},所以AO⊥面BDD_1^{\;}B_1^{\;}$…(3分)
故$∠AGO即为AP与面BDD_1^{\;}B_1^{\;}所成的角$.…(4分)
在Rt△AOG中,tan∠AGO=$\frac{OA}{OG}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{m}{2}}$=3$\sqrt{2}$,即$m=\frac{1}{3}$.
故当$m=\frac{1}{3}$时,直线AP与平面BDD1B1所成的角的正切值为3$\sqrt{2}$.…(6分)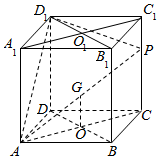
(Ⅱ)依题意,要在A1C1上找一点Q,使得D1Q⊥AP.只需D1Q⊥平面ACC1A1,…(7分)
设A1C1∩B1D1=O1,可推测A1C1的中点$O_1^{\;}$即为所求的Q点.…(8分)
因为$D_1^{\;}O_1^{\;}⊥A_1^{\;}C_1^{\;}$.$D_1^{\;}O_1^{\;}⊥AA_1^{\;}$,
所以D1O1⊥平面ACC1A1,
即D1Q⊥平面ACC1A1,…(10分)
又AP?平面ACC1A1,
故D1O1⊥AP.即D1Q⊥AP.…(12分)
解法二:(1)建立如图所示的空间直角坐标系,…(1分
则A(1,0,0),B(1,1,0),P(0,1,m),
C(0,1,0),D(0,0,0),B1(1,1,1),D1(0,0,1).
所以$\overrightarrow{BD}$=(-1,-1,0),$\overrightarrow{B{B}_{1}}$=(0,0,1),
$\overrightarrow{AP}$═(-1,1,m),
$\overrightarrow{AC}$=(-1,1,0),…(2分)
又由$\overrightarrow{AC}•\overrightarrow{BD}=0,\overrightarrow{AC}•\overrightarrow{BB_1^{\;}}=0知\overrightarrow{AC}为平面BB_1^{\;}D_1^{\;}D$的一个法向量.…(3分)
设AP与$面BDD_1^{\;}B_1^{\;}$所成的角为θ,
则$sinθ=cos(\frac{π}{2}-θ)=\frac{{|\overrightarrow{AP}•\overrightarrow{AC}|}}{{|\overrightarrow{AP}|•|\overrightarrow{AC}|}}=\frac{2}{{\sqrt{2}•\sqrt{{2+m_{\;}^2}}}}$…(4分)
依题意有:$\frac{2}{{\sqrt{2}•\sqrt{{2+m_{\;}^2}}}}=\frac{{3\sqrt{2}}}{{\sqrt{{1+(3\sqrt{2})_{\;}^2}}}}$,解得$m=\frac{1}{3}$.…(5分)
故当$m=\frac{1}{3}$时,直线$AP与平面BDD_1^{\;}B_1^{\;}所成的角的正切值为$$3\sqrt{2}$.…(6分)
(2)若在$A_1^{\;}C_1^{\;}$上存在这样的点Q,设此点的横坐标为x,…(7分)
则$Q(x,1-x,1),\overrightarrow{{D_1}Q}=(x,1-x,0)$.…(8分)
依题意,对任意的m要使D1Q⊥AP,$\overrightarrow{{D}_{1}Q}$$•\overrightarrow{AP}$=-x+(1-x)+0=0,解得x=$\frac{1}{2}$.…(9分)
即C为D的中点时,满足题设的要求.…(12分)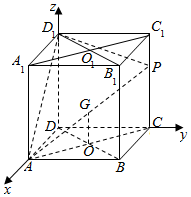
点评 本题考查了空间位置关系、空间角、法向量的性质、向量夹角公式,考查了空间想象能力、推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | y=cos($\frac{π}{2}$+x) | B. | y=-$\frac{2}{x}$ | C. | y=ln$\frac{2-x}{2+x}$ | D. | y=2x-2-x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
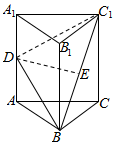 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 30°或150° | D. | 60°或120° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 10 |
| A. | 16个 | B. | 20个 | C. | 24个 | D. | 28个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3n+1}$ | B. | $\frac{n}{3n+1}$ | C. | $\frac{1}{3n-2}$ | D. | $\frac{n}{2(3n+2)}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com