
| x | 11 | 10.5 | 10 | 9.5 | 9 |
| y | 5 | 6 | 8 | 10 | 10 |
| A. | 16个 | B. | 20个 | C. | 24个 | D. | 28个 |
分析 求出样本中心代入回归方程得出$\widehat{a}$,从而得出回归方程解析式,令x=5,计算$\widehat{y}$即可.
解答 解:$\overline{x}$=$\frac{11+10.5+10+9.5+9}{5}=10$,$\overline{y}$=$\frac{5+6+8+10+10}{5}=7.8$.
∴7.8=-3.2×10+$\widehat{a}$,解得$\widehat{a}$=39.8.
∴线性回归方程为$\widehat{y}$=-3.2x+39.8.
当x=5时,$\widehat{y}$=-3.2×5+39.8=23.8≈24.
故选C.
点评 本题考查了线性回归方程的求解即数值预测,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
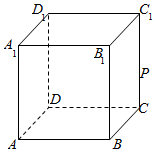 如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 上一年出险次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 下一年保费倍率 | 85% | 100% | 125% | 150% | 175% | 200% |
| 连续两年没出险打7折,连续三年没出险打6折 | ||||||
| 一年中出险的次数 | 0 | 1 | 2 | 3 | 4 | 5次以上(含5次) |
| 频数 | 500 | 380 | 100 | 15 | 4 | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 空气质量指数t | (0,50] | (50,100] | (100,150] | (150,200) | (200,300] | (300,+∞) |
| 质量等级 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天数K | 5 | 23 | 22 | 25 | 15 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com