
分析 (1)根据题意,若A,B,C三点共线,则有$\overrightarrow{AB}$∥$\overrightarrow{AC}$,由向量平行的坐标表示可得(2-k)k+1=0,解可得k的值.
(2)根据题意,△ABC为直角三角形,本题可分三种情形,即A是直角,B是直角或C是直角,由向量垂直的坐标表示分别求出k的值,综合即可得答案.
解答 解:(1)根据题意,若A,B,C三点共线,
则有$\overrightarrow{AB}$∥$\overrightarrow{AC}$,即(2-k)k+1=0,
解可得:k=1±$\sqrt{2}$;
(2)向量$\overrightarrow{AB}$=(2-k,-1),$\overrightarrow{AC}$=(1,k),则$\overrightarrow{BC}$=$\overrightarrow{AC}$-$\overrightarrow{AB}$=(k-1,k+1),
若A是直角,则有$\overrightarrow{AB}$⊥$\overrightarrow{AC}$,则有$\overrightarrow{AB}$•$\overrightarrow{AC}$=(2-k)-k=0,解可得k=1;
若B是直角,则有$\overrightarrow{AB}$⊥$\overrightarrow{BC}$,则有$\overrightarrow{AB}$•$\overrightarrow{BC}$=(2-k)(k-1)-(k+1)=0,此时无解;
若C是直角,则有$\overrightarrow{BC}$⊥$\overrightarrow{AC}$,则有$\overrightarrow{BC}$•$\overrightarrow{AC}$=k2+2k-1=0,解可得k=-1±$\sqrt{2}$,
故k=1或k=-1±$\sqrt{2}$.
点评 本题考查向量数量积的运算以及向量平行的坐标表示,(2)中注意需要进行分类讨论.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:选择题
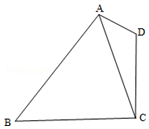
| A. | $\sqrt{7}$ | B. | 2 | C. | 3 | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{\sqrt{2},-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}\}$ | B. | $\{\sqrt{2},\frac{{\sqrt{2}}}{2}\}$ | C. | $\{-\frac{{\sqrt{2}}}{2},\frac{{\sqrt{2}}}{2}\}$ | D. | $\{\sqrt{2},-\frac{{\sqrt{2}}}{2}\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC=$\sqrt{6}$,BC⊥BE,∠ABE=$\frac{π}{3}$.
如图,已知菱形ABEF所在的平面与△ABC所在的平面相互垂直,AB=4,BC=$\sqrt{6}$,BC⊥BE,∠ABE=$\frac{π}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 至少2个白球,都是红球 | B. | 至少1个白球,至少1个红球 | ||
| C. | 至少2个白球,至多1个白球 | D. | 恰好1个白球,恰好2个红球 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
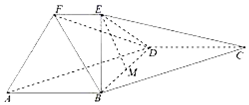 在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.
在如图所示的几何体中,四边形ABCD为平行四边形,∠ABD=90°,EB⊥面ABCD,EF∥AB,AB=2,EB=$\sqrt{3}$的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com