练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过三点A(1,3),B(4,2),C(1,-7)的圆交y轴于M,N两点,则|MN|=（ ）
    A.
    B.8
    C.
    D.10

    【答案】C
    【解析】设圆的方程为x2+y2+Dx+Ey+F=0，则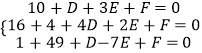

    ∴D=﹣2，E=4，F=﹣20，

    ∴x2+y2﹣2x+4y﹣20=0，

    令x=0，可得y2+4y﹣20=0，

    ∴y=﹣2±2 ，

    ∴|MN|=4 ．

    所以答案是：C．


    【考点精析】利用圆的一般方程对题目进行判断即可得到答案，需要熟知圆的一般方程的特点：(1)①x2和y2的系数相同，不等于0．②没有xy这样的二次项；(2)圆的一般方程中有三个特定的系数D、E、F，因之只要求出这三个系数，圆的方程就确定了；(3)、与圆的标准方程相比较，它是一种特殊的二元二次方程，代数特征明显，圆的标准方程则指出了圆心坐标与半径大小，几何特征较明显．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A、B、C的对边分别为a、b、c，且 ，B=C． （Ⅰ）求cosB的值；
    （Ⅱ）设函数f（x）=sin（2x+B），求 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l1：(a－1)x＋y＋b＝0，l2：ax＋by－4＝0，求满足下列条件的a ， b的值．
    （1）l1⊥l2 ， 且l1过点(1,1)；
    （2）l1∥l2 ， 且l2在第一象限内与两坐标轴围成的三角形的面积为2.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的一元二次不等式ax2+2x+b＞0的解集为{x|x≠c}，则 （其中a+c≠0）的取值范围为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】关于函数f（x）=5sin3x+5 cos3x，下列说法正确的是（ ）
    A.函数f（x）关于x= π对称
    B.函数f（x）向左平移 个单位后是奇函数
    C.函数f（x）关于点（ ，0）中心对称
    D.函数f（x）在区间[0， ]上单调递增

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】求圆心在直线 x 2 y 3 = 0 上，且过点A(2，-3),B(-2，-5)的圆C的方程.
    （1）求圆心在直线 上，且过点A(2，-3),B(-2，-5)的圆C的方程.
    （2）设 是圆C上的点，求 的最大值和最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆C： + =1（a＞b＞0）的焦距为4 ，且椭圆C过点（2 ，1）． （Ⅰ）求椭圆C的方程；
    （Ⅱ）设椭圆C与y轴负半轴的交点为B，如果直线y=kx+1（k≠0）交椭圆C于不同的两点E、F，且B，E，F构成以EF为底边，B为顶点的等腰三角形，判断直线EF与圆x2+y2= 的位置关系．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点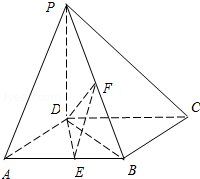
    （1）求证：EF⊥CD；
    （2）在平面PAD内求一点G，使GF⊥平面PCB，并证明你的结论；
    （3）求DB与平面DEF所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设x，y满足约束条件 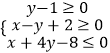，且目标函数z=ax+y仅在点（4，1）处取得最大值，则原点O到直线ax﹣y+17=0的距离d的取值范围是（ ）
    A.（4 ，17]
    B.（0，4 ）
    C.（ ，17]
    D.（0， ）

    查看答案和解析>>

    同步练习册答案