
如图1,在直角梯形ABCD中,AD∥BC,∠ADC=90°,BA=BC.把△BAC沿AC折起到△PAC的位置,使得点P在平面ADC上的正投影O恰好落在线段AC上,如图2所示.点E、F分别为棱PC,CD的中点.
(1)求证:平面OEF∥平面APD;
(2)求证:CD⊥平面POF;
(3)在棱PC上是否存在一点M,使得M到P,O,C,F四点距离相等?请说明理由.

解析: (1)证明:因为点P在平面ADC上的正投影O恰好落在线段AC上,所以PO⊥平面ADC,所以PO⊥AC.
因为AB=BC,所以O是AC的中点,
所以OE∥PA.
同理OF∥AD.
又OE∩OF=O,PA∩AD=A,
所以平面OEF∥平面PDA.
(2)证明:因为OF∥AD,AD⊥CD,
所以OF⊥CD.
又PO⊥平面ADC,CD⊂平面ADC,
所以PO⊥CD.
又OF∩PO=O,所以CD⊥平面POF.
(3)存在,事实上记点E为M即可.
因为CD⊥平面POF,PF⊂平面POF,
所以CD⊥PF.
又E为PC的中点,所以EF=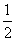 PC,
PC,
同理,在直角三角形POC中,EP=EC=OE=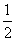 PC,
PC,
所以点E到四个点P,O,C,F的距离相等.


科目:高中数学 来源: 题型:
已知函数f(x)=|x-a|.
(1) 若不等式f(x)≤3的解集为{x|-1≤x≤5},求实数a的值;
(2) 在(1)的条件下,若f(x)+f(x+5)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数y=f(x)的图象关于y轴对称,且当x∈(-∞,0)时,f(x)+xf′(x)<0成立,a=(20.2)·f(20.2),b=(logπ3)·f(logπ3),c=(log39)·f(log39),则a,b,c的大小关系是( )
A.b>a>c B.c>a>b
C.c>b>a D.a>c>b
查看答案和解析>>
科目:高中数学 来源: 题型:
已知常数a,b,c都是实数,f(x)=ax3+bx2+cx-34的导函数为f′ (x),f′(x)≤0的解集为{x|-2≤x≤3},若f(x)的极小值等于-115,则a的值是( )
A.-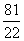 B.
B.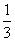
C.2 D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
已知全集U={0,1,2,3,4},A={1,2,3},B={2,4},则如图阴影部分表示的集合为( )
A.{0,2} B.{0,1,3}
C.{1,3,4} D.{2,3,4}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com