
分析 先对函数f(x)进行求导,然后代入f′(x)-9x=0中,再由方程有两根1、4可得两等式;
(1)将a的值代入即可求出b,c的值,再由f(0)=0可求d的值,进而确定函数解析式;
(2)函数f(x)是单调函数,且可判断是单调增函数,再由导函数大于等于0在R上恒成立可解.
解答 解:f′(x)=ax2+2bx+c …(1分)
因为f′(x)-9x=0的两个根分别为1,4,
所以$\left\{\begin{array}{l}{a+2b+c-9=0}\\{16a+8b+c-36=0}\end{array}\right.$ (*) (或:$\left\{\begin{array}{l}1+4=\frac{9-2b}{a}\\ 1×4=\frac{c}{a}\end{array}\right.$即$\left\{\begin{array}{l}2b=9-5a\\ c=4a\end{array}\right.$)…(3分)
(1)当a=3时,由(*)式得$\left\{\begin{array}{l}{2b+c-6=0}\\{8b+c+12=0}\end{array}\right.$,解得:b=-3,c=12(或:$\left\{\begin{array}{l}2b=9-5a=-6\\ c=4a=12\end{array}\right.$)
又因为曲线y=f(x)过原点,所以d=0 故f(x)=x3-3x2+12.…(6分)
(2)由于a>0,所以“f(x)在R上单调”等价于“f'(x)=ax2+2bx+c≥0在R上恒成立”.
只需△=(2b)2-4ac≤0…(8分)
由(*)得$\left\{\begin{array}{l}2b=9-5a\\ c=4a\end{array}\right.$代入整理得,a2-10a+9≤0,…(11分)
解得1≤a≤9.…(12分)
点评 本题主要考查函数的单调性、极值点与其导函数之间的关系.属中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x>0} | B. | {x|x<-3} | C. | {x|-3<x≤-1} | D. | {x|-1<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
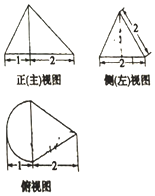
| A. | $\frac{{(4+π)\sqrt{3}}}{3}$ | B. | $\frac{(4+π)\sqrt{3}}{2}$ | C. | $\frac{(4+π)\sqrt{3}}{6}$ | D. | (4+π)$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com