
分析 (1)根据迭代法即可求出数列的通项公式,
(2)根据裂项求和求出bn,再利用定义证明数列{bn}是单调递减数列,即可求出bn的最大值,再解不等式即可求出t的范围
解答 解:(1)a2=6,a3=12
当n≥2时,an=a1+(a2-a1)+(a3-a2)+…+(an-an-1)=2(1+2+3+…+n)=n(n+1)
当n=1时,a1=2也满足上式,
∴an=n(n+1)
(2)${b_n}=\frac{1}{{{a_{n+1}}}}+\frac{1}{{{a_{n+2}}}}+\frac{1}{{{a_{n+3}}}}+…+\frac{1}{{{a_{2n}}}}$,
=$\frac{1}{{({n+1})({n+2})}}+\frac{1}{{({n+2})({n+3})}}$$+…+\frac{1}{{2n({2n+1})}}$,
=$\frac{1}{n+1}-\frac{1}{n+2}+\frac{1}{n+2}-\frac{1}{n+3}+…+\frac{1}{2n}-\frac{1}{2n+1}$,
=$\frac{1}{n+1}-\frac{1}{2n+1}$,
∵${b_{n+1}}-{b_n}=\frac{1}{n+2}-\frac{1}{2n+3}-({\frac{1}{n+1}-\frac{1}{2n+1}})$,
=$\frac{1}{n+2}+\frac{1}{2n+1}-({\frac{1}{n+1}+\frac{1}{2n+3}})$,
=$\frac{3n+3}{{2{n^2}+5n+2}}-\frac{3n+4}{{2{n^2}+5n+3}}<0$,
∴bn+1<bn,
则数列{bn}是单调递减数列,
∴${({b_n})_{max}}={b_1}=\frac{1}{6}$,
∴${t^2}-2t+\frac{1}{6}>{b_n}$$?{t^2}-2t+\frac{1}{6}>\frac{1}{6}$?t2-2t>0?t<0或t>2,
∴t∈(-∞,0)∪(2,+∞)
点评 本题考查了裂项求和、迭代求出数列的通项公式、数列的单调性,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | [2,3] | C. | (0,3] | D. | (2,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
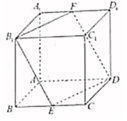 在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.
在正方体ABCD-A1B1C1D1中,E、F分别是BC、A1D1的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com