
【题目】如图1所示,在等腰梯形ABCD中,![]() ,
,![]() ,垂足为E,
,垂足为E,![]() ,
,![]() 将
将![]() 沿EC折起到
沿EC折起到![]() 的位置,如图2所示,使平面
的位置,如图2所示,使平面![]() 平面ABCE.
平面ABCE.
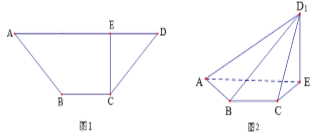
(1)连结BE,证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点G,使得
上是否存在点G,使得![]() 平面
平面![]() ,若存在,直接指出点G的位置
,若存在,直接指出点G的位置![]() 不必说明理由
不必说明理由![]() ,并求出此时三棱锥
,并求出此时三棱锥![]() 的体积;若不存在,请说明理由.
的体积;若不存在,请说明理由.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立的极坐标系中,直线
轴的正半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为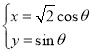 (
(![]() 为参数).
为参数).
(1)写出直线![]() 及曲线
及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且平行于直线
且平行于直线![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() ,
,![]() 两点,若
两点,若![]() ,求点
,求点![]() 的轨迹及其直角坐标方程.
的轨迹及其直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
(1)若函数![]() ,则函数
,则函数![]() 是奇函数;
是奇函数;
(2)![]() ;
;
(3)设函数![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() ;
;
(4)设![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() .
.
A.(2)(3)(4)B.(1)(3)(4)C.(1)(3)D.(1)(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教师调查了![]() 名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
名高三学生购买的数学课外辅导书的数量,将统计数据制成如下表格:
男生 | 女生 | 总计 | |
购买数学课外辅导书超过 |
|
|
|
购买数学课外辅导书不超过 |
|
|
|
总计 |
|
|
|
(Ⅰ)根据表格中的数据,是否有![]() 的把握认为购买数学课外辅导书的数量与性别相关;
的把握认为购买数学课外辅导书的数量与性别相关;
(Ⅱ)从购买数学课外辅导书不超过![]() 本的学生中,按照性别分层抽样抽取
本的学生中,按照性别分层抽样抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人询问购买原因,求恰有
人询问购买原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=1,AD=2,点E、F分别在线段AB、AD上,且EF∥CD,将△AEF沿EF折起到△MEF的位置,并使平面MEF⊥平面BCDFE,得到几何体M﹣BCDEF,则折叠后的几何体的体积的最大值为_____.
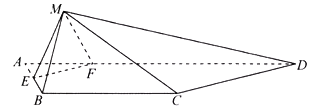
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com