
【题目】在直角坐标系xoy中,已知曲线C:![]() (
(![]() 为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,
为参数),以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,
(1)求曲线C的极坐标方程,若A,B为曲线C上的两点,证明当![]() 时,
时,![]() 定值;
定值;
(2)若过点![]() 且倾斜角为
且倾斜角为![]() 的直线l与曲线C相交于A,B两点,求
的直线l与曲线C相交于A,B两点,求![]() 的值.
的值.
 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知直线l:x![]() y
y![]() 2=0,抛物线C:y2=2px(p>0).
2=0,抛物线C:y2=2px(p>0).
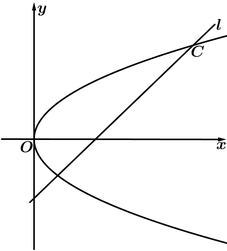
(1)若直线l过抛物线C的焦点,求抛物线C的方程;
(2)已知抛物线C上存在关于直线l对称的相异两点P和Q.
①求证:线段PQ的中点坐标为![]() ;
;
②求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量![]() ,
, ![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)将![]() 的图象向左平移
的图象向左平移![]() (
(![]() )个单位后得到函数
)个单位后得到函数![]() 的图象.若
的图象.若![]() 的图象上各最高点到点
的图象上各最高点到点![]() 的距离的最小值为1,求
的距离的最小值为1,求![]() 的单调增区间.
的单调增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某居民区随机抽取10个家庭,获得第![]() 个家庭的月收入
个家庭的月收入![]() (单位:千元)与月储蓄
(单位:千元)与月储蓄![]() (单位:千元)的数据资料,计算得
(单位:千元)的数据资料,计算得![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)求家庭的月储蓄![]() 关于月收入
关于月收入![]() 的线性回归方程
的线性回归方程![]() ,并判断变量
,并判断变量![]() 与
与![]() 之间是正相关还是负相关;
之间是正相关还是负相关;
(2)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.(注:线性回归方程![]() 中,
中,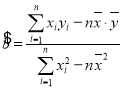 ,其中
,其中![]() ,
,![]() 为样本平均值.)
为样本平均值.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与地面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马,如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.
(1)已知![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长;(精确到
的长;(精确到![]() )
)
(2)求证:四面体![]() 为鳖臑.
为鳖臑.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准:(单位:吨),用水量不超过![]() 的部分按平价收费,超过
的部分按平价收费,超过![]() 的部分按议价收费,为了了解全布市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照
的部分按议价收费,为了了解全布市民用用水量分布情况,通过袖样,获得了100位居民某年的月用水量(单位:吨),将数据按照![]() ……
……![]() 分成9组,制成了如图所示的频率分布直方图
分成9组,制成了如图所示的频率分布直方图
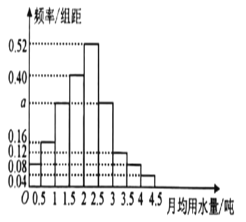
(1)求频率分布直方图中![]() 的值;
的值;
(2)若该市政府看望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由。
的值,并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】化简
(1)![]()
(2)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)切化弦可得三角函数式的值为-1
(2)结合三角函数的性质可得三角函数式的值为![]()
试题解析:
(1)tan70°cos10°( ![]() tan20°﹣1)
tan20°﹣1)
=cot20°cos10°( ![]() ﹣1)
﹣1)
=cot20°cos10°(![]() )
)
=![]() ×cos10°×(
×cos10°×(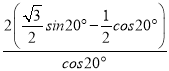 )
)
=![]() ×cos10°×(
×cos10°×(![]() )
)
=![]() ×(﹣
×(﹣![]() )
)
=﹣1
(2)∵(1+tan1°)(1+tan44°)=1+(tan1°+tan44°)+tan1°tan44°
=1+tan(1°+44°)[1﹣tan1°tan44°]+tan1°tan44°=2.
同理可得(1+tan2°)(1+tan43°)
=(1+tan3°)(1+tan42°)
=(1+tan4°)(1+tan41°)=…=2,
故![]() =
=![]()
点睛:三角函数式的化简要遵循“三看”原则:一看角,这是重要一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式 ;二看函数名称,看函数名称之间的差异,从而确定使用的公式,常见的有切化弦;三看结构特征,分析结构特征,可以帮助我们找到变形的方向,如遇到分式要通分等.
【题型】解答题
【结束】
18
【题目】平面内给定三个向量![]()
(1)求![]()
(2)求满足![]() 的实数
的实数![]() .
.
(3)若![]() ,求实数
,求实数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的极坐标方程是
的极坐标方程是![]() ,以极点为原点,以极轴为
,以极点为原点,以极轴为![]() 轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线
轴的正半轴,取相同的单位长度,建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为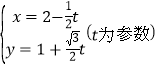 .
.
(1)写出直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设曲线![]() 经过伸缩变换
经过伸缩变换![]() 得到曲线
得到曲线![]() ,曲线
,曲线![]() 上任一点为
上任一点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 分别为左右焦点,
分别为左右焦点,![]() 是椭圆
是椭圆![]() 上点,且
上点,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,则
,则![]() 的内切圆的面积是否存在最大值?若存在,求出这个最大值以及此时的直线方程;若不存在,请说明理由.
的内切圆的面积是否存在最大值?若存在,求出这个最大值以及此时的直线方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com