
【题目】如图,多面体 ABCDEF中,四边形ABCD是边长为2的菱形,且平面ABCD⊥平面DCE.AF∥DE,且AF=![]() DE=2,BF=2
DE=2,BF=2![]() .
.
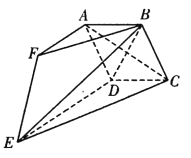
(1)求证:AC⊥BE;
(2)若点F到平面DCE的距离为![]() ,求直线EC与平面BDE所成角的正弦值.
,求直线EC与平面BDE所成角的正弦值.
【答案】(1)见解析;
(2)![]() .
.
【解析】
(1)由题意及勾股数可证得平面![]() 平面
平面![]() ,再由面面垂直的性质可证DE与平面ABCD垂直,可得AC⊥DE,再结合菱形中的垂直证得
,再由面面垂直的性质可证DE与平面ABCD垂直,可得AC⊥DE,再结合菱形中的垂直证得![]() 平面
平面![]() ,从而得到结论;
,从而得到结论;
(2)设![]() ,连接
,连接![]() .由(1)
.由(1)![]() 平面
平面![]() ,则
,则![]() 是
是![]() 在平面
在平面![]() 内的射影,可得
内的射影,可得![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .由点F到平面DCE的距离可得菱形
.由点F到平面DCE的距离可得菱形![]() 中,
中,![]() ,可求得OC,在
,可求得OC,在![]() 中,可求得EC,则可得结果.
中,可求得EC,则可得结果.
(1)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴AC⊥DE.①
∵四边形![]() 为菱形,
为菱形,
∴![]() . ②
. ②
由①②,且![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() .
.
(2)设![]() ,连接
,连接![]() .
.
由(1)![]() 平面
平面![]() ,∴
,∴![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,
∴![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.

∵![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴点![]() 到平面
到平面![]() 的距离等于点
的距离等于点![]() 到平面
到平面![]() 的距离.
的距离.
在平面![]() 内作
内作![]() ,交
,交![]() 延长线于
延长线于![]() .
.
∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∴![]() .(或转化为点
.(或转化为点![]() 到平面
到平面![]() 的距离)
的距离)
∵![]() ,∴
,∴![]() ,
,
∴菱形![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
∴![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某花店每天以每枝![]() 元的价格从农场购进若干枝玫瑰花,然后以每枝
元的价格从农场购进若干枝玫瑰花,然后以每枝![]() 元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进![]() 枝玫瑰花,求当天的利润
枝玫瑰花,求当天的利润![]() (单位:元)关于当天需求量
(单位:元)关于当天需求量![]() (单位:枝,
(单位:枝,![]() )的函数解析式.
)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
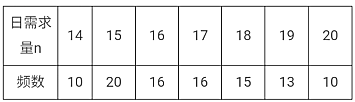
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进![]() 枝玫瑰花,
枝玫瑰花,![]() 表示当天的利润(单位:元),求
表示当天的利润(单位:元),求![]() 的分布列,数学期望及方差;
的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的坐标为
的坐标为![]() ,若点
,若点![]() 是曲线
是曲线![]() 截直线
截直线![]() 所得线段的中点,求
所得线段的中点,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如表:
质量指标值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m≤65 |
等级 | 一等品 | 二等品 | 三等品 |
某企业从生产的这种产品中抽取100件产品作为样本,检测其质量指标值,得到如图所示的频率分布直方图.(同一组数据用该区间的中点值作代表):
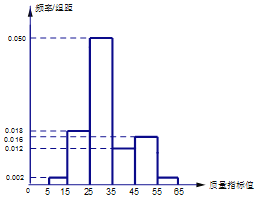
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品82%”的规定?
(2)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值X近似满足X~N(31,122),则“质量提升月”活动后的质量指标值的均值比活动前大约提升或降低多少?
(3)若企业每件一等品售价180元,每件二等品售价150元,每件三等品售价120元,以样本中的频率代替相应概率,现有一名顾客随机购买两件产品,设其支付的费用为X(单位:元),求X的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是离心率为
是离心率为![]() 的椭圆的左、右顶点,
的椭圆的左、右顶点,![]() ,
,![]() 是该椭圆的左、右焦点,
是该椭圆的左、右焦点,![]() ,
,![]() 是直线
是直线![]() 上两个动点,连接
上两个动点,连接![]() 和
和![]() ,它们分别与椭圆交于点
,它们分别与椭圆交于点![]() ,
,![]() 两点,且线段
两点,且线段![]() 恰好过椭圆的左焦点
恰好过椭圆的左焦点![]() .当
.当![]() 时,点
时,点![]() 恰为线段
恰为线段![]() 的中点.
的中点.
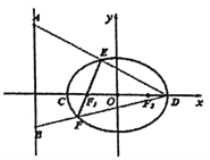
(1)求椭圆的方程;
(Ⅱ)判断以![]() 为直径的圆与直线
为直径的圆与直线![]() 位置关系,并加以证明.
位置关系,并加以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是( )
A.命题“若![]() ⊥
⊥![]() ,则
,则![]()
![]() 0”的否命题为“若
0”的否命题为“若![]() ⊥
⊥![]() ,则
,则![]()
![]() 0”
0”
B.命题“函数f(x)=(a﹣1)x是R上的增函数”的否定是“函数f(x)=(a﹣1)x是R上的减函数”
C.命题“在△ABC中,若sinA=sinB,则A=B”的逆否命题为真命题
D.命题“若x=2,则x2﹣3x+2=0”的逆命题为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,将曲线
,将曲线![]() 向左平移
向左平移![]() 个单位长度得到曲线
个单位长度得到曲线![]() .
.
(1)求曲线![]() 的参数方程;
的参数方程;
(2)已知![]() 为曲线
为曲线![]() 上的动点,
上的动点, ![]() 两点的极坐标分别为
两点的极坐标分别为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的已套指数体系.如图所示的折线图是2017年和2018年的中国仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
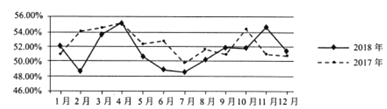
A. 2018年1月至4月的仓储指数比2017年同期波动性更大
B. 这两年的最大仓储指数都出现在4月份
C. 2018年全年仓储指数平均值明显低于2017年
D. 2018年各仓储指数的中位数与2017年各仓储指数中位数差异明显
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为10,则称该数为“完美四位数”,如数字“2017”.试问用数字0,1,2,3,4,5,6,7组成的无重复数字且大于2017的“完美四位数”有( )个.
A. 71B. 66C. 59D. 53
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com