
分析 (1)令F(x)=f(x)-x=(1-mx)ln(1+x)-x,求出函数的导数,通过讨论m的范围,确定函数的单调性,从而确定m的范围即可;
(2)问题等价变形$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$,取$x=\frac{1}{n}(n≥2)$,都有$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$成立;取n=1000即可.
解答 解:(1)令F(x)=f(x)-x=(1-mx)ln(1+x)-x,
则$F'(x)=-mln(1+x)+\frac{1-mx}{1+x}-1$,x∈(0,1),
F″(x)=-$\frac{mx+2m+1}{{(1+x)}^{2}}$,
①当$m≤-\frac{1}{2}$时,由于x∈(0,1),有F″(x)≥0,
于是F'(x)在x∈(0,1)上单调递增,从而F'(x)>F'(0)=0,
因此F(x)在x∈(0,1)上单调递增,即F(x)>0;
②当m≥0时,由于x∈(0,1),有F″(x)<0,
于是F'(x)在x∈(0,1)上单调递减,从而F'(x)<F'(0)=0,
因此F(x)在x∈(0,1)上单调递减,即F(x)<F(0)=0不符;
③当$-\frac{1}{2}<m<0$时,令${x_0}=min\{1,-\frac{2m+1}{m}\}$,当x∈(0,x0]时,
F″(x)<0,于是F'(x)在x∈(0,x0]上单调递减,
从而F'(x)<F'(0)=0,因此F(x)在x∈(0,x0]上单调递减,
即F(x)<F(0)=0而且仅有F(0)=0不符.
综上可知,所求实数m的取值范围是$(-∞,-\frac{1}{2}]$.
证明:(2)对要证明的不等式等价变形如下:
对于任意的正整数n,不等式${(1+\frac{1}{n})^{n+\frac{2}{5}}}<e$恒成立,
等价变形$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$相当于(2)中$m=-\frac{2}{5}$,${x_0}=\frac{1}{2}$的情形,
F(x)在$x∈(0,\frac{1}{2}]$上单调递减,即F(x)<F(0)=0;
取$x=\frac{1}{n}(n≥2)$,都有$(1+\frac{2}{5n})ln(1+\frac{1}{n})-\frac{1}{n}<0$成立;
令n=1000得证.
点评 本题考查了函数的单调性问题,考查导数的应用以及不等式的证明,考查转化思想,分类讨论思想,是一道综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
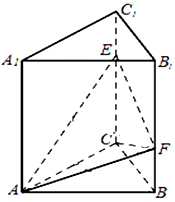 如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.
如图,三棱柱ABC-A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
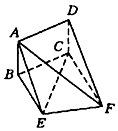 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com