
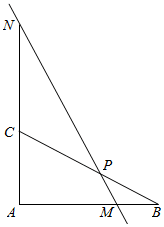
 如图,Rt△ABC中,P是斜边BC上一点,且满足:$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$,点M,N在过点P的直线上,若$\overrightarrow{AM}=λ\overrightarrow{AB},\overrightarrow{AN}=μ\overrightarrow{AC}$,(λ,μ>0),则λ+2μ的最小值为( )
如图,Rt△ABC中,P是斜边BC上一点,且满足:$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$,点M,N在过点P的直线上,若$\overrightarrow{AM}=λ\overrightarrow{AB},\overrightarrow{AN}=μ\overrightarrow{AC}$,(λ,μ>0),则λ+2μ的最小值为( )| A. | 2 | B. | $\frac{8}{3}$ | C. | 3 | D. | $\frac{10}{3}$ |
分析 由已知条件,说明M,P,N三点共线.表示出λ+2μ的表达式,通过求导求关于λ的函数 的最小值即可.
解答 解:若$\overrightarrow{AM}=λ\overrightarrow{AB},\overrightarrow{AN}=μ\overrightarrow{AC}$,(λ,μ>0),
$\overrightarrow{MB}$=$\overrightarrow{MP}$+$\overrightarrow{PB}$=(1-λ)$\overrightarrow{AB}$;
M,P,N三点共线,∴存在实数k,使$\overrightarrow{MP}$=k$\overrightarrow{MN}$=k($\overrightarrow{AN}$-$\overrightarrow{AM}$)=-kλ$\overrightarrow{AB}$+kμ$\overrightarrow{AC}$,
$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{PC}$,$\overrightarrow{PB}$=$\frac{1}{3}$$\overrightarrow{CB}$=$\frac{1}{3}$$\overrightarrow{AB}$-$\frac{1}{3}$$\overrightarrow{AC}$;
∴($\frac{1}{3}$-kλ)$\overrightarrow{AB}$+(kμ-$\frac{1}{3}$)$\overrightarrow{AC}$=(1-λ)$\overrightarrow{AB}$;
∴$\left\{\begin{array}{l}{\frac{1}{3}-kλ=1-λ}\\{kμ-\frac{1}{3}=0}\end{array}\right.$;
由②得,k=$\frac{1}{3μ}$代入①得,$\frac{1}{3}$-$\frac{λ}{3μ}$=1-λ;
∴μ=$\frac{λ}{3λ-2}$;
∴λ+2μ=λ+$\frac{2λ}{3λ-2}$;
设f(λ)=λ+$\frac{2λ}{3λ-2}$,λ>0;
∴f′(λ)=$\frac{9{λ}^{2}-12λ}{(3λ-2)^{2}}$,令f′(λ)=0得,λ=0,或 $\frac{4}{3}$;
∴λ∈(0,$\frac{4}{3}$)时,f′(λ)<0,λ∈($\frac{4}{3}$,+∞)时,f′(λ)>0;
∴λ=$\frac{4}{3}$时,f(λ)取极小值,也是最小值;
∴f(λ)的最小值为$\frac{8}{3}$;
即λ+2μ的最小值为$\frac{8}{3}$.
故选:B.
点评 考查向量在几何中的应用,向量加法、减法运算,共线向量基本定理,以及平面向量基本定理,通过求导求函数的最小值的方法及过程.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{3}{2},\sqrt{3}})$ | B. | $({\frac{{\sqrt{3}}}{2},\frac{3}{2}})$ | C. | $({\frac{3}{2},\sqrt{3}}]$ | D. | $({\frac{{\sqrt{3}}}{2},\sqrt{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=x | B. | y=lnx | C. | y=$\frac{1}{\sqrt{x}}$ | D. | y=10x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
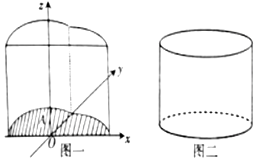 我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.
我国古代数学家祖暅提出原理:“幂势既同,则积不容异”.其中“幂”是截面积,“势”是几何体的高.原理的意思是:夹在两个平行平面间的两个几何体,被任一平行于这两个平行平面的平面所截,若所截的两个截面的面积恒相等,则这两个几何体的体积相等.如图所示,在空间直角坐标系xOy平面内,若函数f(x)=$\left\{\begin{array}{l}\sqrt{1-{x^2}},x∈[{-1,0})\\ cosx,x∈[{0,\frac{π}{2}}]\end{array}$的图象与x轴围成一个封闭的区域A,将区域A沿z轴的正方向平移4个单位,得到几何体如图一,现有一个与之等高的圆柱如图二,其底面积与区域A的面积相等,则此圆柱的体积为π+4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com