
| ωx |
| 2 |
| 3 |
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
| ωx |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| π |
| 3 |
| 2π |
| T |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
| 3 |
| π |
| 3 |
8
| ||
| 5 |
| π |
| 3 |
| 4 |
| 5 |
| 3 |
| π |
| 3 |
| 3 |
| π |
| 3 |
8
| ||
| 5 |


科目:高中数学 来源: 题型:
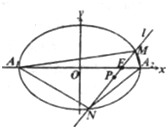 已知椭圆C:
已知椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 6 |
| F(x1)-F(x2) |
| x1-x2 |
| x1+x2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 3 |
| 5 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin(α-3π)•cos(π+α) | ||
cos(2π-α)•sin(-π-α)•sin(
|
| 3π |
| 2 |
| 1 |
| 3 |
| 34 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 8 |
| BM |
| ||
| 2 |
| MN |
| OB |
查看答案和解析>>
科目:高中数学 来源: 题型:
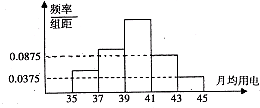 某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图所示;其中直方图从左到右前3个小矩形的面积之比为1:2:3.该乡镇月均用电量在37~39之内的居民共有
某乡镇供电所为了调查农村居民用电量情况,随机抽取了500户居民去年的用电量(单位:kw/h),将所得数据整理后,画出频率分布直方图如图所示;其中直方图从左到右前3个小矩形的面积之比为1:2:3.该乡镇月均用电量在37~39之内的居民共有查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com