
【题目】若对圆 ![]() 上任意一点
上任意一点 ![]() ,
, ![]() 的取值与
的取值与 ![]() 无关,则实数
无关,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]()
【答案】D
【解析】设z=|3x﹣4y+a|+|3x﹣4y﹣9|=5( ![]() ),
),
故|3x﹣4y+a|+|3x﹣4y﹣9|可以看作点P到直线m:3x﹣4y+a=0与直线l:3x﹣4y﹣9=0距离之和的5倍,
∵取值与x,y无关,∴这个距离之和与P无关,
如图所示:可知直线m平移时,P点与直线m,l的距离之和均为m,l的距离,即此时与x,y的值无关,
当直线m与圆相切时, ![]() =1,
=1,
化简得|a﹣1|=5,
解得a=6或a=﹣4(舍去),
∴a≥6
所以答案是:D
【考点精析】根据题目的已知条件,利用点到直线的距离公式和两平行线的距离的相关知识可以得到问题的答案,需要掌握点![]() 到直线
到直线![]() 的距离为:
的距离为: ;已知两条平行线直线
;已知两条平行线直线![]() 和
和![]() 的一般式方程为
的一般式方程为![]() :
:![]() ,
,![]()
![]() ,则
,则![]() 与
与![]() 的距离为
的距离为 .
.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】定义一个集合A的所有子集组成的集合叫做集合A的幂集,记为P(A),用n(A)表示有限集A的元素个数,给出下列命题:①对于任意集合A,都有AP(A);②存在集合A,使得n[P(A)]=3;③用表示空集,若A∩B=,则P(A)∩P(B)=;④若A ![]() B,,则P(A)
B,,则P(A) ![]() P(B);⑤若n(A)-n(B)=1,则n[P(A)]=2×n[P(B)]其中正确的命题个数为( )。
P(B);⑤若n(A)-n(B)=1,则n[P(A)]=2×n[P(B)]其中正确的命题个数为( )。
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)(x∈R)满足f(1)=1,且f(x)的导函数f′(x)< ![]() ,则f(x)<
,则f(x)< ![]() 的解集为( )
的解集为( )
A.{x|-1<x<1}
B.{x|x<-1}
C.{x|x<-1,或x>1}
D.{x|x>1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为 ![]() (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(1)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;
(2)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 是定义在
是定义在 ![]() 上的函数,则“函数
上的函数,则“函数 ![]() 为偶函数”是“函数
为偶函数”是“函数 ![]() 为奇函数”的( )
为奇函数”的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某校高中男生中随机选取100名学生,将他们的体重(单位: ![]() )数据绘制成频率分布直方图,如图所示.
)数据绘制成频率分布直方图,如图所示.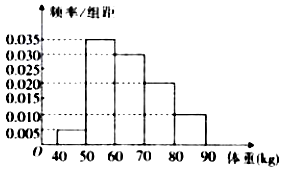
(1)估计该校的100名同学的平均体重(同一组数据以该组区间的中点值作代表);
(2)若要从体重在 ![]() ,
, ![]() ,
, ![]() 三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在
三组内的男生中,用分层抽样的方法选取6人组成一个活动队,再从这6人中选2人当正副队长,求这2人中至少有1人体重在 ![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体 ![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱 ![]() 的中点,过
的中点,过 ![]() 的平面与棱
的平面与棱 ![]() 分别交于点
分别交于点 ![]() .设
.设 ![]() ,
, ![]() .
.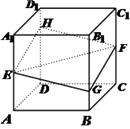
①四边形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四边形
;③四边形 ![]() 的面积
的面积 ![]() 在区间
在区间 ![]() 上具有单调性;④四棱锥
上具有单调性;④四棱锥 ![]() 的体积为定值.
的体积为定值.
以上结论正确的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com