
【题目】如图,四棱锥 ![]() ,底面
,底面 ![]() 为菱形,
为菱形, ![]() 平面
平面 ![]() ,
, ![]() ,
, ![]() 为
为 ![]() 的中点,
的中点, ![]() .
.
(I)求证:直线 ![]() 平面
平面 ![]() ;
;
(II)求直线 ![]() 与平面
与平面 ![]() 所成角的正弦值.
所成角的正弦值.
【答案】(I)证明: ![]() ,
,![]()
又 ![]()
又 ![]() 平面
平面 ![]() ,
, ![]()
![]() 直线
直线 ![]() 平面
平面 ![]() .
.
(II)(方法一)连接 ![]() 过
过 ![]() 点作
点作 ![]() 于
于 ![]() 点.
点.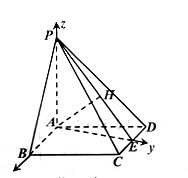
![]() ,
,![]() 平面
平面 ![]() ,
, ![]()
![]() .
.
又 ![]() ,
, ![]() 平面
平面 ![]() .
.
所以 ![]() 为直线
为直线 ![]() 与平面
与平面 ![]() 所成的角.
所成的角.
在 ![]() 中,
中, ![]() ,
, ![]()
![]() 直线
直线 ![]() 与平面
与平面 ![]() 所成角的正弦值为
所成角的正弦值为 ![]()
(方法二)如图建立所示的空间直角坐标系 ![]() .
.![]() .
.![]()
设平面 ![]() 的法向量
的法向量 ![]() ,
,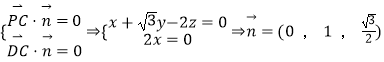
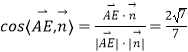 .所以直线
.所以直线 ![]() 与平面
与平面 ![]() 所成角的正弦值为
所成角的正弦值为 ![]()
【解析】(I)推导出AE⊥CD,AE⊥AB,从而PA⊥AE,由此能证明直线AE⊥平面PAB.
(II)(方法一)连接PE,过A点作AH⊥PE于H点,推导出∠AEP为直线AE与平面PCD所成的角,推导出直线AE与平面PCD所成角的正弦值.
(方法二)建立所示的空间直角坐标系A-xyz,由此利用向量法能求出直线AE与平面PCD所成角的正弦值.
【考点精析】本题主要考查了空间中直线与平面之间的位置关系的相关知识点,需要掌握直线在平面内—有无数个公共点;直线与平面相交—有且只有一个公共点;直线在平面平行—没有公共点才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知圆锥曲线 ![]() (
( ![]() 是参数)和定点
是参数)和定点 ![]() ,
, ![]() 、
、 ![]() 是圆锥曲线的左、右焦点.
是圆锥曲线的左、右焦点.
(1)求经过点 ![]() 且垂直于直线
且垂直于直线 ![]() 的直线
的直线 ![]() 的参数方程;
的参数方程;
(2)以坐标原点为极点, ![]() 轴的正半轴为极轴建立极坐标系,求直线
轴的正半轴为极轴建立极坐标系,求直线 ![]() 的极坐标方程.
的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() :
: ![]() 的离心率为
的离心率为 ![]() ,且以两焦点为直径的圆的内接正方形面积为2.
,且以两焦点为直径的圆的内接正方形面积为2.
(1)求椭圆 ![]() 的标准方程;
的标准方程;
(2)若直线 ![]() :
: ![]() 与椭圆
与椭圆 ![]() 相交于
相交于 ![]() ,
, ![]() 两点,在
两点,在 ![]() 轴上是否存在点
轴上是否存在点 ![]() ,使直线
,使直线 ![]() 与
与 ![]() 的斜率之和
的斜率之和 ![]() 为定值?若存在,求出点
为定值?若存在,求出点 ![]() 坐标及该定值,若不存在,试说明理由.
坐标及该定值,若不存在,试说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a·2x+b·3x , 其中常数a,b满足ab≠0.
(1)若ab>0,判断函数f(x)的单调性;
(2)若ab<0,求f(x+1)>f(x)时x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知P为△ABC内一点,且满足 ![]() ,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
,记△ABP,△BCP,△ACP的面积依次为S1 , S2 , S3 , 则S1:S2:S3等于( )
A.1:2:3
B.1:4:9
C.2:3:1
D.3:1:2
查看答案和解析>>
科目:高中数学 来源: 题型:
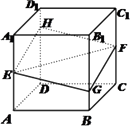
【题目】如图,正方体 ![]() 的棱长为1,
的棱长为1, ![]() 分别是棱
分别是棱 ![]() 的中点,过
的中点,过 ![]() 的平面与棱
的平面与棱 ![]() 分别交于点
分别交于点 ![]() .设
.设 ![]() ,
, ![]() .
.
①四边形 ![]() 一定是菱形;②
一定是菱形;② ![]() 平面
平面 ![]() ;③四边形
;③四边形 ![]() 的面积
的面积 ![]() 在区间
在区间 ![]() 上具有单调性;④四棱锥
上具有单调性;④四棱锥 ![]() 的体积为定值.
的体积为定值.
以上结论正确的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取 ![]() 名同学(男
名同学(男 ![]() 人,女
人,女 ![]() 人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
人),给所有同学几何题和代数题各一题,让各位同学只能自由选择其中一道题进行解答.选题情况如下表(单位:人):
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
附表及公式: ![]()

(1)能否据此判断有 ![]() 的把握认为视觉和空间能力与性别有关?
的把握认为视觉和空间能力与性别有关?
(2)现从选择做几何题的 ![]() 名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为
名女生中,任意抽取两人,对她们的答题情况进行全程研究,记甲、乙两位女生被抽到的人数为 ![]() ,求
,求 ![]() 的分布列和
的分布列和 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com