
【题目】已知函数 ![]() .
.
(1)证明: ![]() ;
;
(2)若对任意 ![]() ,不等式
,不等式 ![]() 恒成立,求实数
恒成立,求实数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:令 ![]() ,则
,则 ![]()
当 ![]() 所以
所以 ![]()
![]()
即 ![]() 在
在 ![]() 递增;在
递增;在 ![]() 递减;
递减;
所以 ![]() ,
, ![]()
(2)解:记 ![]() 则在
则在 ![]() 上,
上, ![]() ,
,![]()
①若 ![]() ,
, ![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 单调递增,
单调递增, ![]() ,
,
这与 ![]() 上
上 ![]() 矛盾;
矛盾;
②若 ![]() ,
, ![]() ,
, ![]() 上
上 ![]() 递增,而
递增,而 ![]() ,这与
,这与 ![]() 上
上 ![]() 矛盾;
矛盾;
③若 ![]() ,
, ![]() ,
, ![]() 时
时 ![]() ,
, ![]() 单调递减;
单调递减; ![]() 时
时 ![]() 单递增;
单递增;
∴ ![]() ,即
,即 ![]() 恒成立;
恒成立;
④若 ![]() ,
, ![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增; ![]() 时,
时, ![]() ,
, ![]() 单调递减,∴
单调递减,∴ ![]() ,这与
,这与 ![]() 上
上 ![]() 矛盾;
矛盾;
⑤若 ![]() ,
, ![]() ,
, ![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增; ![]() 时,
时, ![]() ,
, ![]() 单调递减,∴
单调递减,∴ ![]() 这与
这与 ![]() 上
上 ![]() 矛盾.
矛盾.
综上,实数 ![]() 的取值范围是
的取值范围是 ![]() .
.
【解析】(1)设一个新的函数g(x)= f ( x ) ( x 1 )然后求导,证明其在定义域内小于等于零.
(2)设一个新的函数h(x)=ax+![]() lnx,对a的取值进行讨论,然后判断当h=1时的值是否符合题意.
lnx,对a的取值进行讨论,然后判断当h=1时的值是否符合题意.


科目:高中数学 来源: 题型:
【题目】如图直三棱柱 ![]() 中,
中, ![]() 为边长为2的等边三角形,
为边长为2的等边三角形, ![]() ,点
,点 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 分别是边
分别是边 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的中点,动点
的中点,动点 ![]() 在四边形
在四边形 ![]() 内部运动,并且始终有
内部运动,并且始终有 ![]() 平面
平面 ![]() ,则动点
,则动点 ![]() 的轨迹长度为( )
的轨迹长度为( )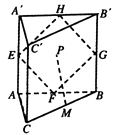
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且a>b,a>c.△ABC的外接圆半径为1, ![]() ,若边BC上一点D满足BD=2DC,且∠BAD=90°,则△ABC的面积为 .
,若边BC上一点D满足BD=2DC,且∠BAD=90°,则△ABC的面积为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某分公司经销某种品牌产品,每件产品的成本为30元,并且每件产品须向总公司缴纳a元(a为常数,2≤a≤5)的管理费,根据多年的统计经验,预计当每件产品的售价为x元时,产品一年的销售量为 ![]() (e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(e为自然对数的底数)万件,已知每件产品的售价为40元时,该产品一年的销售量为500万件.经物价部门核定每件产品的售价x最低不低于35元,最高不超过41元.
(1)求分公司经营该产品一年的利润L(x)万元与每件产品的售价x元的函数关系式;
(2)当每件产品的售价为多少元时,该产品一年的利润L(x)最大,并求出L(x)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断错误的是( )
A.若随机变量 ![]() 服从正态分布
服从正态分布 ![]() ,则
,则 ![]() ;
;
B.若 ![]() 组数据
组数据 ![]() 的散点都在
的散点都在 ![]() 上,则相关系数
上,则相关系数 ![]() ;
;
C.若随机变量 ![]() 服从二项分布:
服从二项分布: ![]() , 则
, 则 ![]() ;
;
D.![]() 是
是 ![]() 的充分不必要条件;
的充分不必要条件;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com