
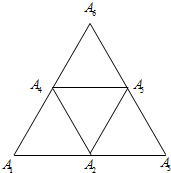
 如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )
如图,由四个边长为1的等边三角形拼成一个边长为2的等边三角形,各项点依次为,A1,A2,A3,…A6则$\overrightarrow{{A_1}{A_2}}•\overrightarrow{{A_j}{A_i}},({i,j∈[{1,2,3,…6}]})$的值组成的集合为( )| A. | {-2,-1,0,1,2} | B. | $\left\{{-2,-1,-\frac{1}{2},0,\frac{1}{2},1,2}\right\}$ | ||
| C. | $\left\{{-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2}}\right\}$ | D. | $\left\{{-2,-\frac{3}{2},-1,-\frac{1}{2},0,\frac{1}{2},1,\frac{3}{2},2}\right\}$ |
分析 通过观察图形知道向量$\overrightarrow{{A}_{j}{A}_{i}}$分成以下三个类型:①小三角形边上的向量,②大三角形边上的向量,③大三角形中线向量,这样求出每种情况下$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{j}{A}_{i}}$的值,从而求得答案.
解答 解:对向量$\overrightarrow{{A}_{j}{A}_{i}}$分成以下几种类型:
边长为1的小三角形边上的向量,只需找一个小三角形A1A2A4,它其它小三角形边上的向量相等;
大三角形A1A3A6边上的向量,和它的中线上的向量,所以有:
$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{2}}=1$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{2}{A}_{1}}=-1$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{4}}=\frac{1}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{4}{A}_{1}}=-\frac{1}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{2}{A}_{4}}=-\frac{1}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{4}{A}_{2}}=\frac{1}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{3}}=2$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{3}{A}_{1}}=-2$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{6}}=1$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{6}{A}_{1}}=-1$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{3}{A}_{6}}=-1,\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{6}{A}_{3}}=1$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{1}{A}_{5}}=\frac{3}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{5}{A}_{1}}=-\frac{3}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{3}{A}_{4}}=-\frac{3}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{4}{A}_{3}}=\frac{3}{2}$,$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{2}{A}_{6}}=\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{6}{A}_{2}}=0$;
∴$\overrightarrow{{A}_{1}{A}_{2}}•\overrightarrow{{A}_{j}{A}_{i}}$所有值组成的集合为{1,-1,$\frac{1}{2},-\frac{1}{2},2,-2,\frac{3}{2},-\frac{3}{2},0$}.
故选:D.
点评 考查相等向量,相反向量的概念,向量数量积的计算公式,等边三角形中线的特点.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (6,3) | B. | (-6,3) | C. | -3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p或q为真,p且q为假,非p为真 | B. | p或q为假,p且q为假,非p为真 | ||
| C. | p或q为真,p且q为假,非p为假 | D. | p或q为假,p且q为真,非p为真 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,一条东西走向的大江,其河岸A处有人要渡江到对岸B处,江面上有一座大桥AC,已知B在A的西南方向,C在A的南偏西15°,BC=10公里.现有两种渡江方案:
如图,一条东西走向的大江,其河岸A处有人要渡江到对岸B处,江面上有一座大桥AC,已知B在A的西南方向,C在A的南偏西15°,BC=10公里.现有两种渡江方案:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1)∪(1,2) | C. | (1,+∞) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 11 | C. | 10 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com