Question

3．圆O为△ABC的外接圆，半径为2，若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$，且|$\overrightarrow{OA}$=|$\overrightarrow{AC}$|，则$\overrightarrow{BA}•\overrightarrow{BO}$=6|

Answer 1

分析 由△ABC外接圆圆心O满足$\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），可得点O在BC上．由于|$\overrightarrow{AO}$|=|$\overrightarrow{AC}$|．可得△OAC是等边三角形，从而求出|$\overrightarrow{BA}$|，|$\overrightarrow{BO}$|的值，求出$\overrightarrow{BA}$•$\overrightarrow{BO}$的值即可．

解答 解：△ABC外接圆半径等于2，其圆心O满足$\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$），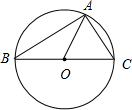
∴点O在BC上，∴∠BAC=90°．
∵|$\overrightarrow{AO}$|=|$\overrightarrow{AC}$|．
∴△OAC是等边三角形．
∴∠ACB=60°，∠B=30°，
∴|$\overrightarrow{BA}$|=2$\sqrt{3}$，|$\overrightarrow{BO}$|=2，
∴$\overrightarrow{BA}$•$\overrightarrow{BO}$=|$\overrightarrow{BA}$|•|$\overrightarrow{BO}$|•cosB=2$\sqrt{3}$•2•$\frac{\sqrt{3}}{2}$=6．

点评 本题考查了三角形外接圆的性质、含30°的直角三角形的边角关系、等边三角形的定义、向量的投影等基础知识与基本技能方法，属于中档题．