
【题目】如图,在梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是矩形,
是矩形, ![]() ,点
,点![]() 在线段
在线段![]() 上.
上.
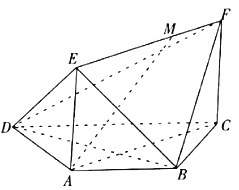
(1)当![]() 为何值时,
为何值时, ![]() 平面
平面![]() ?证明你的结论;
?证明你的结论;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)当![]() 时,根据三角形相似及平行线的性质可证明
时,根据三角形相似及平行线的性质可证明![]() 是矩形,从而得四边形
是矩形,从而得四边形![]() 是平行四边形,所以
是平行四边形,所以![]() ,进而根据相面平行的性质可得结论;(2)以点
,进而根据相面平行的性质可得结论;(2)以点![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,分别求出平面
轴,建立空间直角坐标系,分别求出平面![]() 的一个法向量、平面
的一个法向量、平面![]() 的一个法向量,利用空间向量夹角余弦公式可得结果.
的一个法向量,利用空间向量夹角余弦公式可得结果.
试题解析:(1)当![]() 时,
时, ![]() 平面
平面![]() ,证明如下:
,证明如下:
在梯形![]() 中,设
中,设![]() ,连接
,连接![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ,又
,又![]() ,
,
因为![]() ∽
∽![]() ,
,
因此![]() ,
,
所以![]() ,因为
,因为![]() 是矩形,
是矩形,
所以四边形![]() 是平行四边形,
是平行四边形,
所以![]() ,
,
又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(2)在平面![]() 内过点
内过点![]() 作
作![]() ,
,
因为平面![]() 平面
平面![]() ,且交线为
,且交线为![]() ,
,
则![]() 平面
平面![]() ,即
,即![]() ,
, ![]() ,
,
以点![]() 为原点,分别以
为原点,分别以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则 ,
, ![]() ,
,  ,
, ![]() ,
,
所以![]() ,
,  ,
,  ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,
,
∴ ,取
,取![]() ,
,
同理可得平面![]() 的法向量
的法向量![]() ,
,
所以 ,
,
因为二面角![]() 是锐角,所以其余弦值是
是锐角,所以其余弦值是![]() .
.



 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:
【题目】动点![]() 在圆
在圆![]() :
: ![]() 上运动,定点
上运动,定点![]() ,线段
,线段![]() 的垂直平分线与直线
的垂直平分线与直线![]() 的交点为
的交点为![]() .
.
(Ⅰ)求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)过点![]() 的直线
的直线![]() ,
, ![]() 分别交轨迹
分别交轨迹![]() 于
于![]() ,
, ![]() 两点和
两点和![]() ,
, ![]() 两点,且
两点,且![]() .证明:过
.证明:过![]() 和
和![]() 中点的直线过定点.
中点的直线过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一支车队有![]() 辆车,某天依次出发执行运输任务。第一辆车于下午
辆车,某天依次出发执行运输任务。第一辆车于下午![]() 时出发,第二辆车于下午
时出发,第二辆车于下午![]() 时
时![]() 分出发,第三辆车于下午
分出发,第三辆车于下午![]() 时
时![]() 分出发,以此类推。假设所有的司机都连续开车,并都在下午
分出发,以此类推。假设所有的司机都连续开车,并都在下午![]() 时停下来休息.
时停下来休息.
到下午![]() 时,最后一辆车行驶了多长时间?
时,最后一辆车行驶了多长时间?
如果每辆车的行驶速度都是![]() ,这个车队当天一共行驶了多少
,这个车队当天一共行驶了多少![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立,若数列{an}满足 ![]() ,(n∈N*),且a1=f(0),则下列结论成立的是( )
,(n∈N*),且a1=f(0),则下列结论成立的是( )
A.f(a2013)>f(a2016)
B.f(a2014)>f(a2015)
C.f(a2016)<f(a2015)
D.f(a2014)<f(a2016)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为![]() ,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+
,以原点O为圆心,椭圆的短半轴长为半径的圆与直线x﹣y+![]() =0相切.
=0相切.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若直线l:y=kx+m与椭圆C相交于A、B两点,且kOAkOB=﹣![]() ,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
,判断△AOB的面积是否为定值?若为定值,求出定值;若不为定值,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC是斜三角形,内角A、B、C所对的边的长分别为a、b、c.若csinA= ![]() acosC.
acosC.
(1)求角C;
(2)若c= ![]() ,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
,且sinC+sin(B﹣A)=5sin2A,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,周长为7.5cm,且sinA:sinB:sinC=4:5:6,下列结论:
①a:b:c=4:5:6 ②a:b:c=2: ![]() ③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
③a=2cm,b=2.5cm,c=3cm ④A:B:C=4:5:6
其中成立的个数是( )
A.0个
B.1个
C.2个
D.3个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设![]() 与定点
与定点![]() 的距离和它到直线
的距离和它到直线![]() 的距离的比是常数
的距离的比是常数![]() ,
,
(1)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程:
的方程:
(2)过定点![]() 的直线
的直线![]() 交曲线
交曲线![]() 于
于![]() 两点,以
两点,以![]() 三点(
三点(![]() 为坐标原点)为顶点作平行四边形
为坐标原点)为顶点作平行四边形![]() ,若点
,若点![]() 刚好在曲线
刚好在曲线![]() 上,求直线
上,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教育机构随机某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成[0,5),[5,10),[10,15),[15,20),[20,25),[25,30),[30,35),[35,40]时,所作的频率分布直方图如图所示,则原始茎叶图可能是( ) 
A.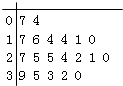
B.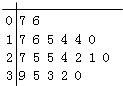
C.
D.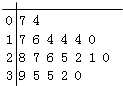
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com