
分析 (Ⅰ)将a=2代入函数f(x),求出其表达式,得到函数的单调区间,从而求出函数的最值;
(Ⅱ)构造函数φ(x)=f(x)+5,通过求导得到函数的极值点,从而得到不等式组,解出即可.
解答 解:(Ⅰ)当a=2时,f(x)=x3+2x2-4x,(a>0),
f′(x)=3x2+4x-4=(x+2)(3x-2),
令f′(x)>0,解得:$x<-2或x>\frac{2}{3}$,
令f′(x)<0,解得:-2<x<$\frac{2}{3}$,
∴函数f(x)的单调递增区间为$({-∞,-2}),({\frac{2}{3},+∞})$,单调递减区间$({-2,\frac{2}{3}})$,
当x=-2时,函数f(x)的极大值f(-2)=8,
当x=$\frac{2}{3}$时,函数f(x)的极小值$f({\frac{2}{3}})=-\frac{40}{27}$;
(Ⅱ)设φ(x)=f(x)+5=x3+ax2-a2x+5,
φ′(x)=3x2+2ax-a2=(x+a)(3x-a),
∴-a,$\frac{a}{3}$是函数f(x)的极值点,
由题意知:$\left\{{\begin{array}{l}{φ(-a)>0}\\{φ(\frac{a}{3})<0}\end{array}}\right.∴a>3$,
综上可知,a的取值范围为:a>3.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{18}$ | B. | $\frac{25}{9}$ | C. | $\frac{25}{3}$ | D. | $\frac{50}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 增函数 | B. | 减函数 | ||
| C. | 常数函数 | D. | 可能是增函数,也可能是常数函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{π}{4},\frac{π}{3}})$ | B. | $({\frac{2π}{3},\frac{5π}{6}})$ | C. | $({0,\frac{π}{3}})∪({\frac{3π}{4},π})$ | D. | $({\frac{π}{3},\frac{2π}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
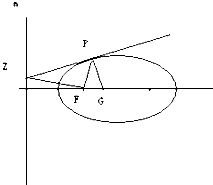 已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.
已知:如图,设P为椭圆上的任意一点,过点P作椭圆的切线,交准线m于点Z,此时FZ⊥FP,过点P作PZ的垂线交椭圆的长轴于点G,椭圆的离心率为e,求证:FG=e•FP.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -m | B. | $-\frac{m}{2}$ | C. | $\frac{m}{2}$ | D. | m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com