练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知F1，F2为椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，M为椭圆C的上顶点，且|MF1|=2，右焦点与右顶点的距离为1．
    （1）求椭圆C的标准方程；
    （2）若直线l与椭圆C相交于A，B两点，且直线OA，OB的斜率kOA，kOB满足kOA•kOB=-$\frac{3}{4}$，求△AOB的面积．

    分析 （1）由椭圆的性质，|MF1|=2，即a=2，a-c=1，即可求得c=1，b2=3，即可求得椭圆的方程；
    （2）当直线l斜率不存在时，kOA•kOB=-$\frac{3}{4}$，求得A和B点坐标，利用三角形面积公式，即可求得△AOB的面积，当直线l的斜率存在，设出直线l的方程，将直线l的方程代入椭圆方程，消去y得到关于x的一元二次方程，根据韦达定理求得x1+x2和x1•x2，根据斜率公式求得表示出kOA•kOB，由点到直线距离公式及三角形面积公式，即可求得△AOB的面积，综上即可求得△AOB的面积．

    解答 解：（1）由题意得，a=2，a-c=1，得c=1，a2=b2+c2，
    ∴b2=3，
    ∴椭圆的方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$，…（3分）
    （2）①当直线l的斜率不存在时，设l：x=n，不妨取A（n，$\sqrt{3（1-\frac{{n}^{2}}{4}）}$），B（n，-$\sqrt{3（1-\frac{{n}^{2}}{4}）}$），
    由kOA•kOB=-$\frac{3}{4}$，解得n2=2．
    此时，S△AOB=$\frac{1}{2}$丨AB丨•丨n丨=$\sqrt{3}$，…（5分）
    ②当直线l的斜率存在时，设l：y=kx+m，A（x1，y1），B（x2，y2），
    由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=kx+m}\end{array}\right.$，消去y化简得：（3+4k2）x2+8kmx+4m2-12=0，
    由韦达定理可知x1+x2=-$\frac{8km}{3+4{k}^{2}}$，x1•x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$，△＞0得4k2-m2+3＞0…（7分）
    kOA•kOB=-$\frac{3}{4}$，$\frac{{y}_{1}y2}{{x}_{1}{x}_{2}}$=-$\frac{3}{4}$，即：3x1•x2+4y1•y2=0，
    即：3x1•x2+4（kx1+m）（kx2+m）=0，
    即：（3+4k2）x1•x2+4km（x1+m2）+4m2=0，
    化简整理得：3+4k2=2m2，…（9分）
    由弦长公式得：丨AB丨=$\sqrt{（1+{k}^{2}）}$•$\sqrt{（{x}_{1}+{x}_{2}）^{2}-4{x}_{1}{x}_{2}}$，
    =$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{48（4{k}^{2}-{m}^{2}+3）}{（3+4{k}^{2}）^{2}}}$，
    O到直线y=kx+m的距离d=$\frac{丨m丨}{\sqrt{1+{k}^{2}}}$，则：
    S△AOB=$\frac{1}{2}$丨AB丨•d=$\sqrt{\frac{12（4{k}^{2}+3-{m}^{2}）}{（3+4{k}^{2}）^{2}}}$丨m丨，
    =$\sqrt{\frac{12（2{m}^{2}-{m}^{2}）}{（2{m}^{2}）^{2}}}$•丨m丨，
    =$\sqrt{3}$．  …（11分）
    综上所述，S△AOB=$\sqrt{3}$．    …（12分）

    点评 本题考查了椭圆的标准方程，考查了直线和圆锥曲线的关系，该题思路清晰，运算复杂，考查了学生的运算能力．属难题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    1．将函数y=f（x）的图象向右平移$\frac{π}{2}$单位得到函数y=cos2x的图象，则f（x）=（　　）
    A．-sin2xB．cos2xC．sin2xD．-cos2x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．执行如图所示的程序框图，输出的S的值为（　　）  
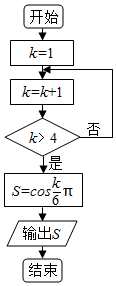
    A．-$\frac{{\sqrt{3}}}{2}$B．$\frac{{\sqrt{3}}}{2}$C．-$\frac{1}{2}$D．$\frac{1}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．一直三棱柱的每条棱长都是3，且每个顶点都在球O的表面上，则球O的表面积为（　　）
    A．21πB．24πC．28πD．36π

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．函数f（x）=4sin2x的最小正周期为（　　）
    A．2πB．πC．$\frac{π}{2}$D．$\frac{π}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知PC为球O的直径，A、B是球面上两点，且AB=2，∠APC=∠BPC=$\frac{π}{4}$，若球O的表面积是16π，则三棱锥P-ABC的体积是（　　）
    A．$\frac{4\sqrt{3}}{3}$B．$4\sqrt{3}$C．$\frac{{2\sqrt{3}}}{3}$D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．定义在（-∞，0）∪（0，+∞）上的函数f（x），总有f（mn）=f（m）f（n），且f（x）＞0，当x＞1时，f（x）＞1．
    （1）求f（1），f（-1）的值；
    （2）判断函数的奇偶性，并证明；
    （3）判断函数在（0，+∞）上的单调性，并证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．焦点在x轴上，且焦点到准线的距离是2的抛物线的标准方程是（　　）
    A．y2=8x或y2=-8xB．x2=8y或x=-8yC．x2=4y或x2=-4yD．y2=4x或y2=-4x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知双曲线C：$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1（a＞0，b＞0），焦距为2c，若l1：y=$\sqrt{3}$（x-c）与C的左右两支交于一点，l2：y=2$\sqrt{2}$（x+c）与C的左支交于两点，则双曲线的离心率的范围是（　　）
    A．（1，3）B．（2，3）C．（1，2）D．（$\sqrt{5}$，3）

    查看答案和解析>>

    同步练习册答案