
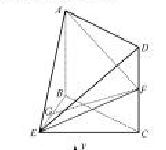
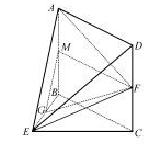
如图,在几何体ABCDE中,四边形ABCD是矩形,AB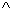 平面BEG,BE
平面BEG,BE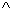 EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
EC,AB=BE=EC=2,G,F分别是线段BE,DC的中点.
(1)求证:GF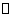 平面ADE
平面ADE
(2)求平面AEF与平面BEC所成锐二面角的余弦值.
 |
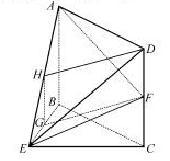 解法一:(1)如图,取AE的中点H,连接HG,HD,
解法一:(1)如图,取AE的中点H,连接HG,HD,
又G是BE的中点,
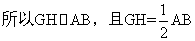 ,
,
又F是CD中点,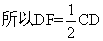 ,
,
由四边形ABCD是矩形得,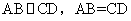 ,
,
所以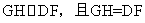 .
.
从而四边形HGFD是平行四边形,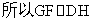 ,
,
又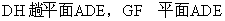 ,所以
,所以 .
.
(2)如图,在平面BEG内,过点B作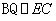 ,因为
,因为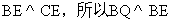
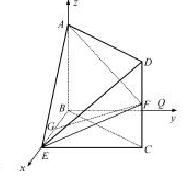 又因为AB
又因为AB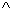 平面BEC,所以AB
平面BEC,所以AB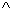 BE,AB
BE,AB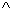 BQ
BQ
以B为原点,分别以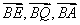 的方向为x轴,y轴,z轴的正方向
的方向为x轴,y轴,z轴的正方向
建立空间直角坐标系,则A(0,0,2),B(0,0,0),E(2,0,0),F(2,2,1)
因为AB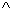 平面BEC,所以
平面BEC,所以 为平面BEC的法向量,
为平面BEC的法向量,
设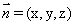 为平面AEF的法向量.又
为平面AEF的法向量.又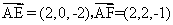
由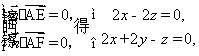 取
取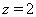 得
得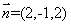 .
.
从而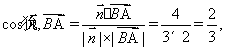
 所以平面AEF与平面BEC所成锐二面角的余弦值为
所以平面AEF与平面BEC所成锐二面角的余弦值为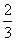 .
.
解法二:(1)如图,取AB中点M,连接MG,MF,
又G是BE的中点,可知GM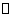 AE,
AE,
又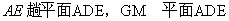 ,
,
所以GM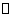 平面ADE.
平面ADE.
在矩形ABCD中,由M,F分别是AB,CD的中点得MF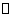 AD.
AD.
又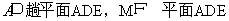 ,所以
,所以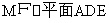 .
.
又因为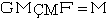 ,
,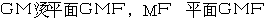
所以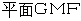
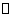 平面ADE,
平面ADE,
因为 ,所以
,所以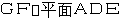
(2)同解法一.


科目:高中数学 来源: 题型:
在平面直角坐标系 中,圆C的参数方程为
中,圆C的参数方程为 .在极坐标系(与平面直角坐标系
.在极坐标系(与平面直角坐标系 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以 轴非负半轴为极轴)中,直线l的方程为
轴非负半轴为极轴)中,直线l的方程为
(1)求圆C的普通方程及直线l的直角坐标方程;
(2)设圆心C到直线l的距离等于2,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
在直角坐标系xOy中,曲线 ,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线
,在以O为极点,x轴正半轴为极轴的极坐标系中,曲线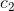 :
: ,曲线
,曲线 :
: .
.
(1).求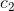 与
与 交点的直角坐标
交点的直角坐标
(2).若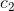 与
与 相交于点A,
相交于点A, 与
与 相交于点B,求
相交于点B,求 的最大值
的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
设a >1,函数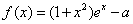
(1)求f(x)的单调区间;
(2)证明f(x)在(- )上仅有一个零点;
)上仅有一个零点;
(3)若曲线y=f(x)在点P处的切线与x轴平等,且在点M(m,n)处的切线与直线OP平等(O是坐标原点),证明: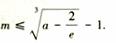
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com