(1)在极坐标系中,已知圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,求实数a的值.
(2)对5副不同的手套进行不放回抽取,甲先任取一只,乙再任取一只,然后甲又任取一只,最后乙再任取一只.对于下列事件:①A:甲正好取得两只配对手套;②B:乙正好取得两只配对手套.试判断事件A与B是否独立?并证明你的结论.
解:(1)p
2=2pcosθ,圆ρ=2cosθ的普通方程为:x
2+y
2=2x,(x-1)
2+y
2=1,
直线3ρcosθ+4ρsinθ+a=0的普通方程为:3x+4y+a=0,
又圆与直线相切,所以
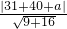
=1,解得:a=2,或a=-8.
(2)设“甲正好取得两只配对手套”为事件A
∵从10只手套中任取4只有C
104种不同的取法,
甲先任取一只要从5对中取一对且一对中又有两种不同的取法,
余下的乙从8只手套中取两只,有C
82中取法,
根据古典概型公式得到
P(A)=
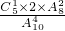
=

.
P(B)=
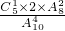
=

.
∵从10只手套中任取4只有C
104种不同的取法,
甲乙两个人都取得成对的手套有C
52×2×C
21×2种不同取法,
∴P(AB)=
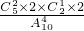
=
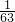
,
又P(A)=

,P(B)=

,
∴P(A)P(B)=

,
∴P(A)P(B)≠P(AB),故A与B是不独立的.
分析:(1)先圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ
2=x
2+y
2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.
(2)从10只手套中任取4只有C
104种不同的取法,甲先任取一只要从5对中取一对且一对中又有两种不同的取法,余下的乙从8只手套中取两只,有C
82中取法,根据古典概型公式得到结果.乙正好取得两只配对手套做法同乙完全相同.要验证两个时间是否独立,只要验证两个概率的乘积是否等于两个事件同时发生的概率,代入解出的结果进行验证.
点评:(1)本小题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力.
(2)对于第(2)小问,手套或鞋子成对问题是概率题目中较困难的问题,可拿一个典型题目认真分析,看清题目解答过程,使得以后遇到知道怎么考虑.本题还考查相互独立事件,一般地,如果事件 相互独立,那么事件同时发生的概率,等于每个事件发生的概率的积.

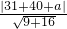 =1,解得:a=2,或a=-8.
=1,解得:a=2,或a=-8.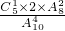 =
= .
.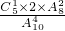 =
= .
.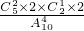 =
=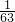 ,
, ,P(B)=
,P(B)= ,
, ,
,

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案