
分析 (1)把a=-1代入函数解析式,求导得到导函数的零点,求得原函数的最值,把f(x)=$\frac{b}{x}$转化为b=xf(x),则b的最小值可求;
(2)求出F′(x)=$\frac{-{x}^{2}+(2-a)x+a-\frac{1}{x}+lnx}{{e}^{x}}$.设h(x)=$-{x}^{2}+(2-a)x+a-\frac{1}{x}+lnx$,可得h′(x)≥2-a.然后分a≤2和a>2研究F(x)在区间(0,1]上是否为单调函数,从而求得a的取值范围.
解答 解:(1)当a=-1时,f(x)=x2+x-lnx,
f′(x)=2x-1-$\frac{1}{x}$=$\frac{(x-1)(2x+1)}{x}$.
当x∈(0,1)时,f′(x)<0,f(x)为减函数;当x∈(1,+∞)时,f′(x)>0,f(x)为增函数.
∴f(x)≥f(1)=0.
由f(x)=$\frac{b}{x}$,得b=xf(x),
又x>0,∴b≥0.
即b的最小值为0;
(2)F(x)=f(x)•e-x,
F′(x)=$\frac{-{x}^{2}+(2-a)x+a-\frac{1}{x}+lnx}{{e}^{x}}$.
设h(x)=$-{x}^{2}+(2-a)x+a-\frac{1}{x}+lnx$.
则h′(x)=-2x+$\frac{1}{{x}^{2}}+\frac{1}{x}+2-a$,可知h′(x)在(0,1]上为减函数.
从而h′(x)≥h′(1)=2-a.
①当2-a≥0,即a≤2时,h′(x)≥0,h(x)在区间(0,1]上为增函数,
∵h(1)=0,∴h(x)≤0在区间(0,1]上恒成立,即F′(x)≤0在区间(0,1]上恒成立.
∴F(x)在区间(0,1]上是减函数,故a≤2满足题意;
②当2-a<0,即a>2时,设函数h′(x)的唯一零点为x0,则h(x)在(0,x0)上单调递增,在(x0,1)上单调递减.
又∵h(1)=0,∴h(x0)>0.
∴F(x)在(x0,1)上单调递增,
∵h(e-a)<0,∴F(x)在(0,e-a)上递减,这与F(x)在区间(0,1]上是单调函数矛盾.
∴a>2不合题意.
综合①②得:a≤2.
点评 本题考查利用导数研究函数的单调性,考查分类讨论的数学思想方法,考查逻辑思维能力与推理运算能力,难度较大.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}x=2+t\\ y=1-t\end{array}\right.(t$为参数) | B. | $\left\{\begin{array}{l}x=1-\sqrt{t}\\ y=1+\sqrt{t}\end{array}\right.(t$为参数) | ||
| C. | $\left\{\begin{array}{l}x=3+t\\ y=-1-t\end{array}\right.(t$为参数) | D. | $\left\{\begin{array}{l}x=1-{t^2}\\ y=1+{t^2}\end{array}\right.(t$为参数) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
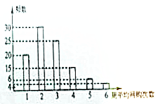 网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.
网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁.| 网购迷 | 非网购迷 | 合计 | |
| 年龄不超过40岁 | |||
| 年龄超过40岁 | |||
| 合计 |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
| k0 | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com