
���� �� I �����æ�2=x2+y2����sin��=y��������Cת����ֱ�����귽�̣���ֱ��l����ͨ����x-y=m����F����ֱ�߷��̣��������m�����ֱ��l����ͨ���̣�
�����ɣ� I ����֪������ԲC���ڽӾ����ڵ�һ���Ķ��㣨2cos�ȣ�$\sqrt{2}$sin�ȣ�����L=2��4cos��+2$\sqrt{2}$sin�ȣ�=4$\sqrt{6}$sin����+�գ����������Һ��������ʣ��������L�����ֵ��
��� �⣺�� I ��������C�ļ����귽�̣���2=$\frac{4}{1+si{n}^{2}��}$������2+��2sin2��=4��
����2=x2+y2����sin��=y��������ʽ�����������ã�$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$��
ֱ��l����ͨ����Ϊx-y=m����F����ֱ�߷��̣���m=$\sqrt{2}$��
��ֱ��l����ͨ����Ϊx-y+$\sqrt{2}$=0��
��������ԲC���ڽӾ����ڵ�һ���Ķ��㣨2cos�ȣ�$\sqrt{2}$sin�ȣ�����0���ȣ�$\frac{��}{2}$����
����ԲC���ڽӾ��ε��ܳ�L=2��4cos��+2$\sqrt{2}$sin�ȣ�=4$\sqrt{6}$sin����+�գ���tan��=$\sqrt{2}$��
������C���ڽӾ��ε��ܳ�ΪL����ֵΪ4$\sqrt{6}$��
���� ���⿼�������������ͨ���̵�ת������Բ�ļ����귽�̼��������̵�Ӧ�ã����鸨���ǹ�ʽ��Ӧ�ã����Һ�������ֵ��������������������е��⣮


 ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д�
ѧ�����νӽ̲��Ͼ���ѧ������ϵ�д� Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5��}{6}$ | B�� | $\frac{3��}{4}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
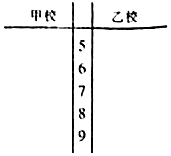 ij�жԴ����м�ʾ����ѧУ���ļס�������ѧУ���и������գ���ѧ����������һ���������������20λ������20λ�����������ѧУ�����֣�����Խ�߱������������Խ�ã����������£�
ij�жԴ����м�ʾ����ѧУ���ļס�������ѧУ���и������գ���ѧ����������һ���������������20λ������20λ�����������ѧУ�����֣�����Խ�߱������������Խ�ã����������£��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com