
分析 (1)利用递推关系可得an,再利用对数的运算性质可得bn.
(2)利用“错位相减法”与等比数列的前n项和公式、数列的单调性即可得出.
解答 解:(1)Sn=2-an,n∈N*,∴n=1时,a1=2-a1,解得a1=1.n≥2时,an=Sn-Sn-1=2-an-(2-an-1),化为:an=$\frac{1}{2}{a}_{n-1}$,
∴数列{an}是等比数列,首项为1,公比为$\frac{1}{2}$.
∴an=$(\frac{1}{2})^{n-1}$.
函数f(x)=log${\;}_{\frac{1}{2}}$x,且满足bn=f(an)-3.
∴bn=$lo{g}_{\frac{1}{2}}(\frac{1}{2})^{n-1}$-3=n-4.
(2)cn=an•bn=(n-4)×$(\frac{1}{2})^{n-1}$.
∴{cn}的前n项和为Tn=-3-2×$\frac{1}{2}$-$(\frac{1}{2})^{2}$+0+…+(n-4)×$(\frac{1}{2})^{n-1}$.
$\frac{1}{2}$Tn=$-3×\frac{1}{2}$-2×$(\frac{1}{2})^{2}$+…+(n-5)×$(\frac{1}{2})^{n-1}$+(n-4)×$(\frac{1}{2})^{n}$,
∴$\frac{1}{2}{T}_{n}$=$-3+\frac{1}{2}+(\frac{1}{2})^{2}$+…+$(\frac{1}{2})^{n-1}$-(n-4)×$(\frac{1}{2})^{n}$=$-4+\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$-(n-4)×$(\frac{1}{2})^{n}$=-2-(n-2)×$(\frac{1}{2})^{n}$,
∴Tn=-4-$\frac{n-2}{{2}^{n-1}}$.
∴Tn+1-Tn=$-4-\frac{n-1}{{2}^{n}}$-$(-4-\frac{n-2}{{2}^{n-1}})$=$\frac{n-3}{{2}^{n}}$,
∴n≤3时,Tn+1≤Tn;n≥4时,Tn+1>Tn.
即T1>T2>T3=T4<T5<….
∴Tn的最小值是T3=T4=$-\frac{17}{4}$.
点评 本题考查了递推关系、对数的运算性质、“错位相减法”、等比数列的前n项和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
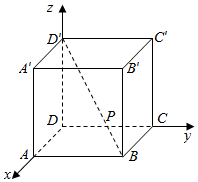
| A. | ($\frac{1}{3}$$,\frac{1}{3}$,$\frac{1}{3}$) | B. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | C. | ($\frac{5}{6}$,$\frac{5}{6}$,$\frac{1}{6}$) | D. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{11}{2}$ | B. | -$\frac{31}{6}$ | C. | $\frac{11}{2}$ | D. | $\frac{31}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com