
分析 (1)根据数量积列方程解出k;
(2)代入两点间的距离公式计算.
解答 解:(1)∵$\overrightarrow{OA•}\overrightarrow{OB}$=-15.
∴-3+f(1)f(-3)=-15,即-3-k$•\frac{k}{3}$=-15.
又k>0,∴k=6.
∴f(1)=k=6,f(-3)=-$\frac{k}{3}$=-2.
∴A(-1,6),B(3,-2).
(2)|$\overrightarrow{AB}$|=|AB|=$\sqrt{(3+1)^{2}+(-2-6)^{2}}$=4$\sqrt{5}$.
点评 本题考查了平面向量的数量积运算,向量的模长公式,属于基础题.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:填空题
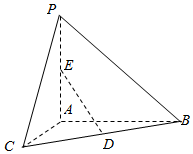 如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.
如图,已知PA⊥平面ABC,AC⊥AB,AP=BC,∠CBA=30°,D、E分别是BC、AP的中点,则异面直线AC与DE所成角的大小为$arccos\frac{{\sqrt{2}}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.55 | B. | 0.6 | C. | 0.65 | D. | 0.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
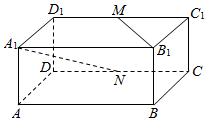 长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )
长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,M、N分别是C1D1、CD的中点,则异面直线A1N和B1M所成角的余弦值为( )| A. | $\frac{\sqrt{30}}{10}$ | B. | 0 | C. | $\frac{\sqrt{15}}{10}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m?β,则α∥β | B. | 若m∥α,m∥β,则α∥β | C. | 若m⊥α,m∥β,则α⊥β | D. | 若m⊥α,m⊥β,则α⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
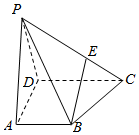 如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.
如图,四棱锥P-ABCD的底面ABCD是梯形,AB∥CD,且AB=$\frac{2}{3}$CD,试问在PC上能否找到一点E,使得BE∥平面PAD?若能,请确定点E的位置,并给出证明;若不能,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com