
分析 分别求出命题p和命题q为真命题时,a的取值范围,再求出p,q全为假命题时,a的取值范围,进而可得p,q至少有一个是真命题,实数a的取值范围.
解答 解:若命题p为真命题,
即关于x的不等式x2+(a-1)x+a2≤0的解集为∅,
则△=(a-1)2-4a2<0,
解得:a∈(-∞,-1)∪($\frac{1}{3}$,+∞),
若命题q为真命题,
即函数y=(2a2-a)x为增函数,
则2a2-a>1,
解得:a∈(-∞,-$\frac{1}{2}$)∪(1,+∞),
若p,q全为假命题,
则a∈[-$\frac{1}{2}$,$\frac{1}{3}$],
故p,q至少有一个是真命题时,
a∈(-∞,-$\frac{1}{2}$)∪($\frac{1}{3}$,+∞)
点评 本题考查的知识点是命题的真假判断与应用,复合命题,二次不等式的解法,指数函数的图象和性质,难度中档.


科目:高中数学 来源: 题型:解答题
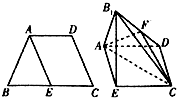 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x-1}$ | B. | y=-x2+2x-1 | C. | y=log2(1-x) | D. | y=2${\;}^{\frac{1}{x}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com