
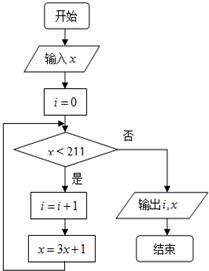
 运行如图所示的程序流程图.
运行如图所示的程序流程图.| 第i次 | i=1 | i=2 | i=3 | i=4 | i=5 |
| x= | 7 | 22 | 67 | 202 | 607 |
分析 (1)模拟执行程序框图,依次写出每次循环得到的x的值即可.
(2)任取两个数,共有10种不同的取法,其平均数分别是:14.5、37、104.5、307、44.5、112、314.5、134.5、337、404.5,设A表示“两个数的平均数大于211”,则A={(7,607),(22,607),(67,607),(202,607)},其平均数分别是307、314.5、337、404.5满足条件,即可得解.
(3)由题意可得该程序执行了循环体2次,解不等式组$\left\{\begin{array}{l}x≤211\\ 3x+1≤211\\ 3(3x+1)+1>211\end{array}\right.$即可得解.
解答 (本小题满分14分)
解:(1)
| 第i次 | i=1 | i=2 | i=3 | i=4 | i=5 |
| x= | 7 | 22 | 67 | 202 | 607 |
点评 本题主要考查了循环结构的程序框图,概率及不等式的解法,综合性较强,属于基本知识的考查.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
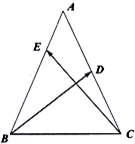 如图,在△ABC中,已知AB=AC=$\sqrt{6}$,AD=DC,$\overrightarrow{AB}$=3$\overrightarrow{AE}$,若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$,则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$.
如图,在△ABC中,已知AB=AC=$\sqrt{6}$,AD=DC,$\overrightarrow{AB}$=3$\overrightarrow{AE}$,若$\overrightarrow{BD}•\overrightarrow{AC}$=-$\frac{1}{2}$,则$\overrightarrow{BD}•\overrightarrow{CE}$等于$-\frac{11}{12}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | φ=$\frac{π}{3}$ | B. | φ=$\frac{π}{4}$ | C. | φ=$\frac{π}{5}$ | D. | φ=$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向右平行移动$\frac{π}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{π}{6}$个单位长度 | D. | 向右平行移动$\frac{π}{6}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -9 | C. | 9 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com