
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 设P(x,y),要使∠APB=90°,只要求出P到AB中点的距离以及圆上的所有点到AB中点距离范围.
解答 解:设P(x,y),要使∠APB=90°,那么P到AB中点(-1,2)的距离为$\sqrt{(x+1)^{2}+(y-2)^{2}}=\frac{1}{2}AB=\sqrt{5}$,
而圆上的所有点到AB中点距离范围为[$\sqrt{(3+1)^{2}+(4-2)^{2}}-\sqrt{5}$,$\sqrt{(3+1)^{2}+(4-2)^{2}}+\sqrt{5}$],即[$\sqrt{5}$,3$\sqrt{5}$],
所以使∠APB=90°的点P的个数只有一个,就是AB中点与圆心连线与圆的交点;
故选B
点评 本题考查了点与圆的位置关系的判断;关键是明确线段AB中点与圆上点的距离范围.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
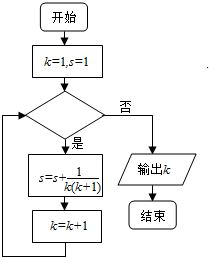
| A. | k<2012 | B. | k<2013 | C. | k<2014 | D. | k<2015 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2π}{3}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 钝角三角形 | ||
| C. | 直角三角形 | D. | 上述三种情况都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
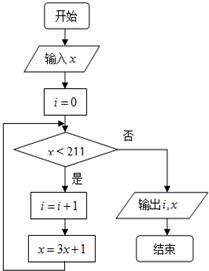 运行如图所示的程序流程图.
运行如图所示的程序流程图.| 第i次 | i=1 | i=2 | i=3 | i=4 | i=5 |
| x= | 7 | 22 | 67 | 202 | 607 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com