
(本小题满分12分)
已知函数 其中
其中 ,
,
(I)若 求
求 的值;(4分)
的值;(4分)
(Ⅱ)在(I)的条件下,若函数 的图像的相邻两条对称轴之间的距离等于
的图像的相邻两条对称轴之间的距离等于 ,
,
① 求函数 的解析式;(4分)②求最小正实数
的解析式;(4分)②求最小正实数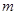 ,使得函数
,使得函数 的图象向左平移
的图象向左平移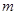 个单位时对应的函数是偶函数.(4分)
个单位时对应的函数是偶函数.(4分)
(I) . (Ⅱ)最小正实数
. (Ⅱ)最小正实数 。
。
解析试题分析:(I)利用特殊角的三角函数值化简cos  cosφ-sin
cosφ-sin  ,sinφ=0,根据|φ|<
,sinφ=0,根据|φ|<  ,直接求出φ的值;
,直接求出φ的值;
(Ⅱ)解法一:在(I)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于 ,求出周期,求出ω,得到函数f(x)的解析式;函数f(x)的图象向左平移m个单位所对应的函数是偶函数.推出m=
,求出周期,求出ω,得到函数f(x)的解析式;函数f(x)的图象向左平移m个单位所对应的函数是偶函数.推出m= (k∈Z),可求最小正实数m.
(k∈Z),可求最小正实数m.
解法二:在(I)的条件下,若函数f(x)的图象的相邻两条对称轴之间的距离等于 
,求出周期,求出ω,得到函数f(x)的解析式;利用g(x)是偶函数当且仅当g(-x)=g(x)对x∈R恒成立,使得函数f(x)的图象向左平移m个单位所对应的函数是偶函数.化简cos(3m+  )=0,然后再求最小正实数m.
)=0,然后再求最小正实数m.
解法一:(I)由 得
得 ……2分
……2分
即 又
又 .………………4分
.………………4分
(Ⅱ)①由(I)得, ………………5分
………………5分
依题意, 又
又 .………………7分
.………………7分
故 ……………………8分
……………………8分
②函数 的图象向左平移
的图象向左平移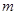 个单位后所对应的函数为
个单位后所对应的函数为 …9分
…9分 是偶函数当且仅当
是偶函数当且仅当 ………………10分
………………10分
即 ,从而,最小正实数
,从而,最小正实数 .……………………12分
.……………………12分
解法二:(I)同解法一………………4分
(Ⅱ)由(I)得, 依题意,
依题意,
又 ,故
,故 ………………8分
………………8分
函数 的图像向左平移
的图像向左平移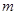 个单位后所对应的函数为
个单位后所对应的函数为
 是偶函数当且仅当
是偶函数当且仅当 对
对 恒成立……………9分
恒成立……………9分
亦即 对
对 恒成立。
恒成立。

即 对
对 恒成立。
恒成立。 ……………………10分
……………………10分
故
 ……………………11分
……………………11分
从而,最小正实数 ……………………12分
……………………12分
考点:本试题主要考查了三角函数的字母变量的求法,三角函数的图象的平移,偶函数的性质,转化思想的应用,考查计算能力,是常考题,中档试题。
点评:解决该试题的关键是利用两角和差的公式得到第一问的值,对于第二问,要熟练运用三角函数的性质得到。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com