
分析 根据不等式的基本性质,判断题目中命题的真假性即可.
解答 解:对于①,若ab>0,则$\frac{1}{ab}$>0
又a>b,
∴$\frac{1}{b}$>$\frac{1}{b}$,∴$\frac{1}{a}$<$\frac{1}{b}$,∴①正确;
对于②,若a>|b|≥0,则a2>b2,∴②正确;
对于③,若a>b,c>d,则-c<-d,
∴-d>-c,∴a-d>b-c,
∴a-c>b-d不成立,③错误;
对于④,对于正数a,b,m,
若a<b,则$\frac{a}{b}<\frac{a+m}{b+m}$成立,
即a(b+m)<b(a+m)
∴am<bm,
∴a<b,④正确;
综上,正确的命题序号是①②④.
故答案为:①②④.
点评 本题考查了不等式的基本性质与应用问题,也考查了命题真假的判断问题,是中档题.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 成功(人) | 失败(人) | 合计 | |
| 20~30(岁) | 20 | 40 | 60 |
| 30~40(岁) | 50 | ||
| 合计 | 70 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 364 | B. | 365 | C. | 728 | D. | 730 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
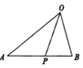 如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )
如图,在△OAB,点P在边AB上,且AP:PB=5:3,则$\overrightarrow{OP}$=( )| A. | $\frac{5}{8}$$\overrightarrow{OB}$+$\frac{3}{8}$$\overrightarrow{OA}$ | B. | $\frac{5}{8}$$\overrightarrow{OA}$+$\frac{3}{8}$$\overrightarrow{OB}$ | C. | $\frac{5}{8}$$\overrightarrow{OB}$-$\frac{3}{8}$$\overrightarrow{OA}$ | D. | $\frac{5}{8}$$\overrightarrow{OA}$-$\frac{3}{8}$$\overrightarrow{OB}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com