
分析 (1)当a,b>0,利用基本不等式可得:$\frac{a+b}{2}$≥$\sqrt{ab}$,上式两边同时取对数即可证明.
(2)利用分析法证明即可.
解答 (1)证明:当a,b>0,有$\frac{a+b}{2}$≥$\sqrt{ab}$,
上式两边同时取对数,有$lg\frac{a+b}{2}$≥$lg\sqrt{ab}$=$\frac{lga+lgb}{2}$,
∴原求证式成立..
(2)证明:(分析法)
欲证ac+bd≤$\sqrt{{(a}^{2}+{b}^{2})({c}^{2}+{d}^{2})}$,
只需证(ac+bd)2≤(a2+b2)(c2+d2),
即证a2c2+2abcd+b2d2≤a2c2+b2d2+a2d2+b2c2,
即证2abcd≤a2d2+b2c2,
即证0≤(bc-ad)2,
而a,b,c,d∈(0,+∞),0≤(bc-ad)2显然成立,
故原不等式成立.
点评 本题考查了基本不等式的性质、分析法、对数的运算性质,考查了推理能力与计算能力,属于中档题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
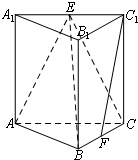 如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1、BC的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,E、F分别为A1C1、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com