练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．为提高市场销售业绩，某公司设计两套产品促销方案（方案1运作费用为5元/件；方案2的运作费用为2元/件），并在某地区部分营销网点进行试点（每个试点网点只采用一种促销方案），运作一年后，对比该地区上一年度的销售情况，分别统计相应营销网点个数，制作相应的列联表如表所示．
    无促销活动采用促销方案1采用促销方案2
    本年度平均销售额不高于上一年度平均销售额48113190
    本年度平均销售额高于上一年度平均销售额526929150
    1008060
    （Ⅰ）请根据列联表提供的信息，为该公司今年选择一套较为有利的促销方案（不必说明理由）；
    （Ⅱ）已知该公司产品的成本为10元/件（未包括促销活动运作费用），为制定本年度该地区的产品销售价格，统计上一年度的8组售价xi（单位：元/件，整数）和销量yi（单位：件）（i=1，2，…8）如表所示：
    售价x3335373941434547
    销量y840800740695640580525460
    （ⅰ）请根据下列数据计算相应的相关指数R2，并根据计算结果，选择合适的回归模型进行拟合；
    （ⅱ）根据所选回归模型，分析售价x定为多少时？利润z可以达到最大．
    $\hat y=-1200lnx+5000$$\hat y=-27x+1700$$\hat y=-\frac{1}{3}{x^2}+1200$
    $\sum_{i=1}^8{（{y_i}}-{\hat y_i}{）^2}$49428.7411512.43175.26
    $\sum_{i=1}^8{（{y_i}}-\overline y{）^2}$124650
    参考公式：相关指数M．

    分析 （I）根据本年度平均销售额高于上一年度平均销售额时，两种方案的采用数量对比进行选择；
    （II）（i）代入相关指数公式计算即可，并选择相关指数最大的模型；
    （ii）求出利润关于售价的函数关系式，利用导数求出函数的极大值点即可．

    解答 解：（Ⅰ）由列联表信息可知，年度平均销售额与方案1的运作相关性强于方案2．
    （Ⅱ）（ⅰ）由已知数据可知，回归模型$\hat y=-1200lnx+5000$对应的相关指数R12=1-$\frac{49428.74}{124650}$=0.6035；
    回归模型$\hat y=-27x+1700$对应的相关指数R22=1-$\frac{11512.43}{124650}$=0.9076；
    回归模型$\hat y=-\frac{1}{3}{x^2}+1200$对应的相关指数R32=1-$\frac{175.26}{124650}$=0.9986．
    因为$R_3^2＞R_2^2＞R_1^2$，所以采用回归模型$\hat y=-\frac{1}{3}{x^2}+1200$进行拟合最为合适．
    （ⅱ）由（Ⅰ）可知，采用方案1的运作效果较方案2好，
    故年利润$z=（-\frac{1}{3}{x^2}+1200）（x-15）$，z'=-（x+30）（x-40），
    当x∈（0，40）时，$z=（-\frac{1}{3}{x^2}+1200）（x-15）$单调递增；
    当x∈（40，+∞）时，$z=（-\frac{1}{3}{x^2}+1200）（x-15）$单调递减．
    故当售价x=40时，利润达到最大．

    点评 本题考查了回归分析，回归模型的比较，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    7．已知直线l的参数方程为$\left\{\begin{array}{l}{x=2-\frac{2\sqrt{5}}{5}t}\\{y=1+\frac{\sqrt{5}}{5}t}\end{array}\right.$（t为参数），曲线C：$\frac{{x}^{2}}{4}$+y2=1
    （1）求直线l的普通方程和曲线C的参数方程；
    （2）若点M在曲线C上运动，试求出M到直线l的距离的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=|2x-a|+|x-1|，a∈R．
    （Ⅰ）若不等式f（x）≥2-|x-1|恒成立，求实数a的取值范围；
    （Ⅱ）当a=1时，直线y=m与函数f（x）的图象围成三角形，求m的最大值及此时围成的三角形的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．在平面直角坐标系xOy中，若直线$l：\left\{\begin{array}{l}x=t\\ y=t-a\end{array}\right.$（t为参数）过椭圆$C：\left\{\begin{array}{l}x=3cosφ\\ y=2sinφ\end{array}\right.$（φ为参数）的右顶点，则常数a的值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．设$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$均为非零向量，若|（$\overrightarrow{a}$+$\overrightarrow{b}$）•$\overrightarrow{c}$|=|（$\overrightarrow{a}$-$\overrightarrow{b}$）•$\overrightarrow{c}$|，则（　　）
    A．$\overrightarrow{a}$∥$\overrightarrow{b}$B．$\overrightarrow{a}$⊥$\overrightarrow{b}$C．$\overrightarrow{a}$∥$\overrightarrow{c}$或$\overrightarrow{b}$∥$\overrightarrow{c}$D．$\overrightarrow{a}$⊥$\overrightarrow{c}$或$\overrightarrow{b}$⊥$\overrightarrow{c}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

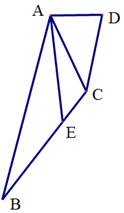    2．在四边形ABCD中，点E在BC上，∠BAD=$\frac{2π}{3}$，AD：AC：CD=1：2：$\sqrt{3}$．
    （1）求∠BAC；
    （2）若AB=1，BE=3EC，AE平分∠BAC，求AE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．执行如图所示的程序框图，输出S的值等于（　　）
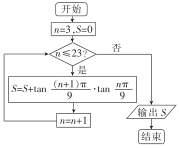
    A．$-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-21$B．$\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-22$
    C．$-\frac{{2\sqrt{3}}}{{tan\frac{π}{9}}}-22$D．$\frac{{tan\frac{25π}{9}-\sqrt{3}}}{{tan\frac{π}{9}}}-21$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．如图中流程图的运行结果是6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知y=f（x）是二次函数，方程f（0）=1，且f′（x）=2x+2
    （1）求f（x）的解析式．
    （2）求函数y=f（x）与y=-x2-4x+1所围成的图形的面积．

    查看答案和解析>>

    同步练习册答案