
分析 (1)t=3,①依题意,${a}_{{n}_{1}}$,${a}_{{n}_{1}+1}$,${a}_{{n}_{1}+2}$成等差数列,根据等差数列等差中项及通项公式,分类讨论当n1为奇数或偶数时,分别求得n1的值;
②a1,an2,an3成等差数列,根据等差中项可知:$2[{{2^{n_2}}-{{(-1)}^{n_2}}}]=3+{2^{n_3}}-{(-1)^{n_3}}$,分别当n2,n3为奇数或偶数时,即可求得n3-n2=1,因此n3-n2为定值;
(2)设as,ar,at(s<r<t)成等差数列,根据数列等差中项定义,2s+2t-2r+1=(-1)s+(-1)t-2(-1)r,分类讨论t=r+1,求得s的值,当t≥r+2,求得s的值,最后求得a1,ar,ar+1成等差数列或a2,ar,ar+1成等差数列,其中r为奇数,即可求得t的最大值.
解答 解:(1)①依题意,${a}_{{n}_{1}}$,${a}_{{n}_{1}+1}$,${a}_{{n}_{1}+2}$成等差数列,即2${a}_{{n}_{1}+1}$=${a}_{{n}_{1}}$+${a}_{{n}_{1}+2}$,
从而$2[{{2^{{n_1}+1}}-{{(-1)}^{{n_1}+1}}}]={2^{n_1}}-{(-1)^{n_1}}+{2^{{n_1}+2}}-{(-1)^{{n_1}+2}}$,
当n1为奇数时,解得${2^{n_1}}=-4$,不存在这样的正整数n1;
当n1为偶数时,解得${2^{n_1}}=4$,所以n1=2.(3分)
②依题意,a1,an2,an3成等差数列,即2an2=a1+an3,
从而$2[{{2^{n_2}}-{{(-1)}^{n_2}}}]=3+{2^{n_3}}-{(-1)^{n_3}}$,
当n2,n3均为奇数时,${2^{n_2}}-{2^{{n_3}-1}}=1$,左边为偶数,故矛盾;
当n2,n3均为偶数时,${2^{{n_2}-1}}-{2^{{n_3}-2}}=1$,左边为偶数,故矛盾;
当n2为偶数,n3奇数时,${2^{{n_2}+1}}-{2^{n_3}}=5$,左边为偶数,故矛盾;
当n2为奇数,n3偶数时,${2^{{n_2}+1}}-{2^{n_3}}=0$,即n3-n2=1.(8分)
(2)设as,ar,at(s<r<t)成等差数列,则2ar=as+at,
即2[2r-(-1)r]=2s-(-1)s+2t-(-1)t,
整理得,2s+2t-2r+1=(-1)s+(-1)t-2(-1)r,
若t=r+1,则2s=(-1)s+-3(-1)r,因为2s≥2,所以(-1)s+-3(-1)r只能为2或4,
所以s只能为1或2;(12分)
若t≥r+2,则2s+2t-2r+1≥2s+2r+2-2r+1≥2+24-23=10,(-1)s+(-1)t-2(-1)r≤4,
故矛盾,
综上,只能a1,ar,ar+1成等差数列或a2,ar,ar+1成等差数列,其中r为奇数,
从而t的最大值为3.(16分)
点评 本题考查了等差数列的通项公式及等差中项的定义,考查分类讨论思想,考查推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (0,0) | B. | (1,0) | C. | (1,-3) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | $\frac{2\sqrt{2}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 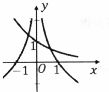 | B. | 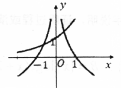 | C. | 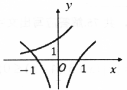 | D. | 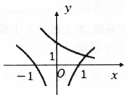 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com