
【题目】已知抛物线C:![]() 的焦点为F,直线l过点
的焦点为F,直线l过点![]() ,交抛物线于A、B两点.
,交抛物线于A、B两点.
(1)若P为![]() 中点,求l的方程;
中点,求l的方程;
(2)求![]() 的最小值.
的最小值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)方法一:利用点差法求中点弦所在直线斜率,再根据点斜式得结果;注意验证所求直线与抛物线有两个交点;
方法二:设中点弦所在直线方程,与抛物线方程联立,利用韦达定理以及中点坐标公式求中点弦所在直线斜率,再根据点斜式得结果;注意考虑中点弦直线斜率不存在的情况是否满足题意;
(2)由抛物线的定义转化![]() ,方法一:设直线l:
,方法一:设直线l:![]() ,与抛物线方程联立,利用韦达定理以及二次函数性质求最值,注意比较直线斜率不存在的情况
,与抛物线方程联立,利用韦达定理以及二次函数性质求最值,注意比较直线斜率不存在的情况![]() 的值;方法二:设直线l:
的值;方法二:设直线l:![]() ,与抛物线方程联立,利用韦达定理以及二次函数性质求最值,此种设法已包含直线斜率不存在的情况.
,与抛物线方程联立,利用韦达定理以及二次函数性质求最值,此种设法已包含直线斜率不存在的情况.
解:(1)方法一:设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,化简得
,化简得![]() ,
,
因为![]() 的中点为
的中点为![]() ,
,![]() ,
,
![]() ,∴l的方程为
,∴l的方程为![]() ,即
,即![]() .
.
经检验,符合题意.
方法二:设![]() ,
,![]() ,
,
当斜率不存在时,显然不成立.
当斜率存在时,设直线l:![]() ,显然
,显然![]() ,
,
由 得
得![]()
易知![]() ,
,![]() ,
,
因为![]() 的中点为
的中点为![]() ,
,![]() ,即
,即![]() ,
,
解得![]() ,∴l的方程为
,∴l的方程为![]()
(2)方法一:由抛物线的定义可知![]()
当斜率不存在时,直线l:![]() ,
,![]()
当斜率存在时,设直线l:![]() ,显然
,显然![]() ,
,
由 得
得![]() ,
,
易知![]() ,
,
 ,
,
![]() 时,
时,![]() 的最小值为
的最小值为![]()
综上,![]() 的最小值为
的最小值为![]()
方法二:由抛物线的定义可知![]()
显然直线l不平行于x轴,设直线l:![]() ,
,
由 得
得![]() ,
,
易知![]() ,
,![]() ,
,![]() ,
,
![]()

![]() 时,
时,![]() 的最小值为
的最小值为![]()


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】(1)经统计,在某储蓄所一个营业窗口排队等候的人数及相应概率如下:
排队人数 | 0 | 1 | 2 | 3 | 4 | 5人及5人以上 |
概率 |
|
|
|
|
|
|
求至少3人排队等候的概率是多少?
(2)在区间![]() 上随机取两个数m,n,求关于x的一元二次方程
上随机取两个数m,n,求关于x的一元二次方程![]() 有实根的概率.
有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是腾讯开发的一个记录跑步或行走情况(步数里程)的公众号用户通过该公众号可查看自己某时间段的运动情况.某人根据2018年1月至2018年11月期间每月离步的里程(单位:十公里)的数据绘制了下面的折线图.根据该折线图,下列结论正确的是( )

A.月跑步里程逐月增加
B.月跑步里程最大值出现在10月
C.月跑步里程的中位数为5月份对应的里程数
D.1月至5月的月跑步里程相对于6月至11月波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为![]() 个
个![]() 销售利润为
销售利润为![]() 元.
元.
(i)求关于![]() 的函数关系式;
的函数关系式;
(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分,某考试每道都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道能排除两个错误选项,另2题只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机挑选一个选项做答,且各题做答互不影响.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,点
是菱形,点![]() 在线段PC上,且三棱锥
在线段PC上,且三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 的体积的
的体积的![]() ,
,![]() ,
,![]() 平面
平面![]() .
.
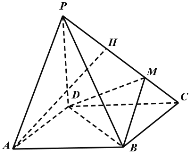
(1)若![]() 是
是![]() 的中点,证明:直线
的中点,证明:直线![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com