Question

3．以双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右顶点A为圆心作与渐近线相切的圆，过左焦点F作该圆的切线，设切点为P，切线与y轴的交点为M，且FM：MP=8：3，求双曲线的离心率．

Answer 1

分析 由题意可推出FM=$\frac{8}{11}$FP，从而可得FP=$\sqrt{\frac{11}{8}（a+c）c}$，再求得r=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$，从而利用勾股定理可得（a+c）²=$\frac{11}{8}$（a+c）c+$\frac{{a}^{2}{b}^{2}}{{c}^{2}}$；从而解得．

解答 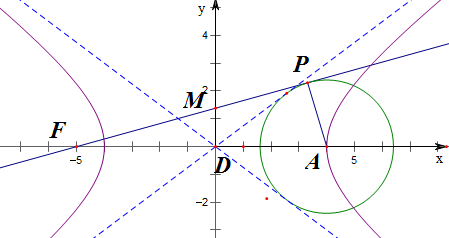解：∵$\frac{FM}{MP}$=$\frac{8}{3}$，
∴$\frac{FM}{FP}$=$\frac{8}{11}$，
即FM=$\frac{8}{11}$FP；
又∵△FMD∽△FAP，
∴$\frac{FD}{FP}$=$\frac{FM}{FA}$，
∴FP=$\sqrt{\frac{11}{8}（a+c）c}$，
A（a，0），
∴r=$\frac{ab}{\sqrt{{a}^{2}+{b}^{2}}}$=$\frac{ab}{c}$，
又∵FA²=FP²+PA²，
∴（a+c）²=$\frac{11}{8}$（a+c）c+$\frac{{a}^{2}{b}^{2}}{{c}^{2}}$；
即3e⁴-5e³-8=（e+1）（e-2）（3e²-2e+4）=0，
解得，e=-1（舍去）或e=2；
故双曲线的离心率为2．

点评 本题考查了双曲线的性质及应用，化简比较困难，属于中档题．