
分析 (I)利用导数的几何意义可得切线的斜率,即可得出切线的方程.
(Ⅱ)设h(x)=f(x)-g(x)=lnx-x+1,利用导数研究其单调性极值与最值即可得出.
(Ⅲ)?x∈(1,+∞),f(x)>0,g(x)>0.对a分类讨论,利用导数研究其单调性极值与最值即可得出.
解答 解:(Ⅰ)f′(x)=$\frac{1}{x}$,∴f′(1)=1,又f(1)=0,
得切线l:y-0=1×(x-1),即y=x-1.
证明:(Ⅱ)设h(x)=f(x)-g(x)=lnx-x+1,则h′(x)=$\frac{1}{x}$-1,令h′(x)=0,得x=1.
| x | (0,1) | 1 | (1,+∞) |
| h′(x) | + | 0极大值 | - |
| h(x) | 单调递增 | 0 | 单调递减 |
| x | $(0,\frac{1}{a})$ | $\frac{1}{a}$ | $(\frac{1}{a},+∞)$ |
| u′(x) | + | 0 | - |
| u(x) | 单调递增 | 0 | 单调递减 |
点评 本题考查了利用导数研究其单调性极值与最值、导数的几何意义,考查了分类讨论、推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:选择题
已知函数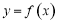 的定义域为
的定义域为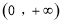 ,当
,当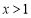 时,
时,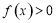 ,对任意的
,对任意的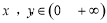 ,
,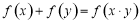 成立,若数列
成立,若数列 满足
满足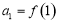 ,且
,且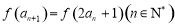 ,则
,则 的值为( )
的值为( )
A.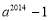 B.
B.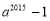 C.
C. D.
D.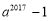
查看答案和解析>>
科目:高中数学 来源:2017届河北沧州市高三9月联考数学(理)试卷(解析版) 题型:选择题
甲、乙、丙、丁四位同学各自在周六、周日两天中随机选一天郊游,则周六、周日都有同学参加郊游的情况共有( )
A.2种 B.10种 C.12种 D.14种
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com