
分析 (1)设l:y=kx+b,由$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}=8y-1}\end{array}\right.$,得x2-8kx-8b+1=0,由此利用韦达定理、导数性质,结合已知条件能求出l的方程为y=kx+$\frac{17}{8}$,恒过定点(0,$\frac{17}{8}$).
(2)设M(u,v),直线MA:$\frac{{x}_{1}}{4}x-y-{y}_{1}+\frac{1}{4}=0$,由此可得切线AB的方程为$\frac{x}{4}u-y-v+\frac{1}{4}$=0,由直线AB与圆相切得${v}^{2}-\frac{{u}^{2}}{16}=1$,由此能求出存在两个定点T1(0,-1),T2(0,1),满足${k}_{M{T}_{1}}•{k}_{M{T}_{2}}$=$\frac{1}{16}$恒为定值.
解答 证明:(1)依题意,直线l的斜率存在,设l:y=kx+b,A(x1,y1),B(x2,y2),
由$\left\{\begin{array}{l}{y=kx+b}\\{{x}^{2}=8y-1}\end{array}\right.$,得x2-8kx-8b+1=0,
则x1x2=-8b+1,…(2分)
又由y=$\frac{{x}^{2}+1}{8}$,得${y}^{'}=\frac{x}{4}$,
${k}_{MA}•{k}_{MB}=\frac{{x}_{1}}{4}•\frac{{x}_{2}}{4}=-1$,x1x2=-16,
∴-8b+1=-16,∴b=$\frac{17}{8}$,…(4分)
∴l的方程为y=kx+$\frac{17}{8}$,恒过定点(0,$\frac{17}{8}$).…(5分)
解:(2)设M(u,v),直线MA:y-y1=$\frac{{x}_{1}}{4}$(x-x1),即$\frac{{x}_{1}}{4}x-y-{y}_{1}+\frac{1}{4}=0$,
又MA经过M(u,v),∴$\frac{{x}_{1}}{4}u-v-{y}_{1}+\frac{1}{4}=0$,即$\frac{{x}_{1}}{4}u-{y}_{1}-v+\frac{1}{4}$=0,
∴$\frac{{x}_{1}}{4}u-{y}_{2}-v+\frac{1}{4}=0$,
由此可得切线AB的方程为$\frac{x}{4}u-y-v+\frac{1}{4}$=0,…(8分)
由直线AB与圆相切得$\frac{|0×\frac{u}{4}-\frac{1}{4}-v+\frac{1}{4}|}{\sqrt{(\frac{u}{4})^{2}+1}}$=1,化简得${v}^{2}-\frac{{u}^{2}}{16}=1$,…(10分)
从而动点M的轨迹方程为${y}^{2}-\frac{{x}^{2}}{16}=1$,为焦点在y轴上的双曲线.
取T1(0,-1),T2(0,1),则${k}_{M{T}_{1}}•{k}_{M{T}_{2}}$=$\frac{y+1}{x}•\frac{y-1}{x}$=$\frac{{y}^{2}-1}{{x}^{2}}$=$\frac{\frac{{x}^{2}}{16}}{{x}^{2}}$=$\frac{1}{16}$为定值
故存在两个定点T1(0,-1),T2(0,1),满足${k}_{M{T}_{1}}•{k}_{M{T}_{2}}$=$\frac{1}{16}$恒为定值.…(12分)
点评 本题考查直线恒过定点的证明及定点坐标的求法,考查两直线的斜率之积恒为定值的定点是否存在的判断与求法,解题时要认真审题,注意韦达定理、导数数性质、直线方程、圆的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
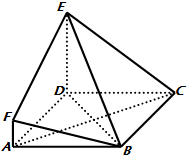 在如图所示的几何体中,四边形ABCD是边长为3的菱形,∠DAB=60°,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
在如图所示的几何体中,四边形ABCD是边长为3的菱形,∠DAB=60°,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一或第三象限角 | B. | 第二或第三象限角 | ||
| C. | 第一或第四象限角 | D. | 第二或第四象限角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com