练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．若$\frac{1+2i}{z}=i$，则z的虚部为（　　）
    A．-1B．1C．-2D．2

    分析 由$\frac{1+2i}{z}=i$，得$z=\frac{1+2i}{i}$，然后利用复数代数形式的乘除运算化简复数z，则z的虚部可求．

    解答 解：由$\frac{1+2i}{z}=i$，
    得$z=\frac{1+2i}{i}$=$\frac{-i（1+2i）}{-{i}^{2}}=2-i$，
    则z的虚部为：-1．
    故选：A．

    点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2017届河北沧州市高三9月联考数学（理）试卷（解析版） 题型：选择题

    甲、乙、丙、丁四位同学各自在周六、周日两天中随机选一天郊游，则周六、周日都有同学参加郊游的情况共有（ ）

    A．2种 B．10种 C．12种 D．14种

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．若某空间几何体的三视图如图所示，则该几何体是（　　）
    A．三棱柱B．三棱锥C．四棱锥D．四棱台

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．F是抛物线x2=2y的焦点，A、B是抛物线上的两点，|AF|+|BF|=6，则线段AB的中点到x轴的距离为2.5．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知各项均为正数的等比数列{an}的前n项和为Sn，若a3a7=16a5，a3+a5=20，则（　　）
    A．Sn=2an-1B．Sn=2an-2C．Sn=4-2anD．Sn=3-2an

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知曲线C1：x2+（y-$\frac{1}{4}$）2=1（y≥$\frac{1}{4}$），C2：x2=8y-1（|x|≥1），动直线l与C2相交于A，B两点，曲线C2在A，B处的切线相交于点M．
    （1）当MA⊥MB时，求证：直线l恒过定点，并求出定点坐标；
    （2）若直线l与C1相切于点P，试问：在y轴上是否存在两个定点T1，T2，当直线MT1，MT2斜率存在时，两直线的斜率之积恒为定值？若存在求出满足条件的点T1，T2的坐标，若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

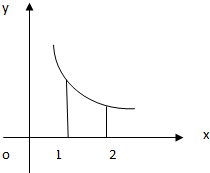    18．已知函数f（x）在区间（0，+∞）上的图象如图所示，记r=f′（1），p=f′（2），q=f（2）-f（1）．则r、p、q之间的大小关系为（　　）
    A．r＜p＜qB．q＜p＜rC．r＜q＜pD．p＜q＜r

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．复数z对应的点A落在虚轴的正半轴上，i为虚数单位且$|{\frac{z+i}{i}}|=2$，则z=（　　）
    A．iB．$\sqrt{3}i$C．2iD．3i

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    16．利用计算机产生0～2之间的均匀随机数x，则事件“3x-2≥0”发生的概率为$\frac{2}{3}$．

    查看答案和解析>>

    同步练习册答案