Question

【题目】【2017届湖南省长沙市高三上学期统一模拟考试文数】已知过的动圆恒与轴相切，设切点为是该圆的直径．

（Ⅰ）求点轨迹的方程；

（Ⅱ）当不在y轴上时，设直线与曲线交于另一点，该曲线在处的切线与直线交于点．求证: 恒为直角三角形．

Answer 1

【答案】(1) ；(2) 证明见解析．

【解析】试题分析：（Ⅰ）设点 ，点是点在 轴射影的中点，即 ，根据几何关系可知 ，将其转化为数量积的坐标表示即为轨迹方程；（Ⅱ）设直线的方程为 与抛物线方程联立，交于两点，设 ，根据导数的几何意义求和两点的直线斜率求 ,证明 ，即说明是直角三角形.

试题解析：(Ⅰ) 设点坐标为，则点坐标为．

因为是直径，所以，或、均在坐标原点．

因此 ,而 ， ，

故有，即，

另一方面，设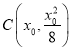是曲线上一点，

则有，

中点纵坐标为，

故以为直径的圆与 轴相切．

综上可知点轨迹的方程为．

(Ⅱ)设直线的方程为，

由得：

设 ，则有．

由对求导知，

从而曲线E在P处的切线斜率，

直线的斜率，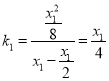

于是 ．

因此 ．

所以恒为直角三角形．