练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    8．某几何体的三视图如图所示，则该几何体的体积是（　　）
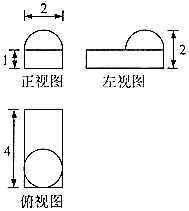
    A．8+$\frac{4}{3}$πB．8+$\frac{2}{3}$πC．4+$\frac{4π}{3}$D．4+$\frac{2π}{3}$

    分析 由已知中的三视图可得：该几何体是一个四棱柱与半球的组合体，进而得到答案．

    解答 解：由已知中的三视图可得：该几何体是一个四棱柱与半球的组合体，
    故体积V=1×2×4+$\frac{1}{2}$×$\frac{4}{3}π$=8+$\frac{2}{3}$π，
    故选：B．

    点评 本题考查的知识点是球的体积与表面积，棱柱的体积与表面积，简单几何体的三视图，难度中档．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    18．已知中心在原点，焦点在x轴上的椭圆的一个顶点坐标为（0，1），其离心率为$\frac{\sqrt{6}}{3}$
    （1）求椭圆的标准方程；
    （2）椭圆上一点P满足∠F1PF2=60°，其中F1，F2为椭圆的左右焦点，求△F1PF2的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

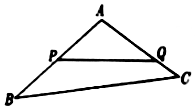    19．如图，某生态园将一块三角形地ABC的一角APQ开辟为水果园，已知角A为120°，AB，AC的长度均大于200米，现在边界AP，AQ处建围墙，在PQ处围竹篱笆．
    （1）若围墙AP、AQ总长度为200米，如何可使得三角形地块APQ面积最大？
    （2）已知竹篱笆长为50$\sqrt{3}$米，AP段围墙高1米，AQ段围墙高2米，造价均为每平方米100元，若AP≥AQ，求围墙总造价的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

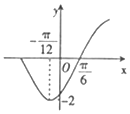    3．设函数f（x）=cos2x-$\sqrt{3}$sin2x，把y=f（x）的图象向左平移$φ（{|φ|＜\frac{π}{2}}）$个单位后，得到的部分图象如图所示，则f（φ）的值等于（　　）
    A．$-\sqrt{3}$B．$\sqrt{3}$C．-1D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知一组数据（2，3），（4，6），（6，9），（x0，y0）的线性回归方程为$\stackrel{∧}{y}$=x+2，则x0-y0的值为（　　）
    A．2B．4C．-4D．-2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数f（x）=x$（{{e^x}-\frac{1}{e^x}}）$，若f（x1）＜f（x2），则（　　）
    A．x1＞x2B．x1＜x2C．${x}_{1}^{2}$＜${x}_{2}^{2}$D．x1+x2=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．将二项式${（x+\frac{2}{{\sqrt{x}}}）^6}$展开式各项重新排列，则其中无理项互不相邻的概率是（　　）
    A．$\frac{2}{7}$B．$\frac{1}{35}$C．$\frac{8}{35}$D．$\frac{7}{24}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．如图所示的算法流程图中，输出S的值为49．

    查看答案和解析>>

    同步练习册答案