
 如图,设正棱锥S-ABC的体积为6,E,F和G分别是SA、AB和BC的中点,已知二面角E-FG-A的平面角为60°,求SA.
如图,设正棱锥S-ABC的体积为6,E,F和G分别是SA、AB和BC的中点,已知二面角E-FG-A的平面角为60°,求SA. 分析 设0点为定点S在底面ABC内的射影,由S-ABC是正三棱锥,构造出二面角的平面角,再根据体积公式,即可求出答案.
解答 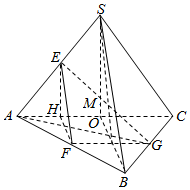 解:设0点为定点S在底面ABC内的射影,由S-ABC是正三棱锥,
解:设0点为定点S在底面ABC内的射影,由S-ABC是正三棱锥,
所以0为△ABC的中心,A,O,G在一条直线上,且E在底面上的射影H也在AG上,
设M是AC的中心,由于AB=BC,SA=SC,从而AC⊥BM,AC⊥SM,
所以AC⊥SB,
又EF∥AB,FG∥AC,于是得EF⊥FG,
再由FG⊥EH,可得FG⊥HF,
所以∠EFH是二面角E-FG-A的平面角,
所以∠EFH=60°,
记为a,SA=m,则AO=$\frac{\sqrt{3}}{3}$a,SO=$\sqrt{{m}^{2}-\frac{1}{3}{a}^{2}}$,
EH=$\frac{1}{2}$SO=$\frac{1}{2}$$\sqrt{{m}^{2}-\frac{1}{3}{a}^{2}}$,EF=$\frac{1}{2}$SB=$\frac{1}{2}$SA=$\frac{1}{2}$m,
由此得sinα=$\frac{EH}{EF}$=$\frac{\sqrt{{m}^{2}-\frac{1}{3}{a}^{2}}}{m}$,即a=$\sqrt{3}$mcosα,
三棱锥的体积V=$\frac{1}{3}$•$\frac{\sqrt{3}}{4}$a2$\sqrt{{m}^{2}-\frac{1}{3}{a}^{2}}$=$\frac{\sqrt{3}}{4}$m3cos2αsinα,
所以m=$\root{3}{\frac{4\sqrt{3}v}{3sinαco{s}^{2}α}}$,
由V=6,α=60°,从而m=sa=4.
点评 本题考查了二面角的平面的求法,以及三棱锥的体积公式,培养了学生的转化能力,推理能力,属于难题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{14}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{14}+\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
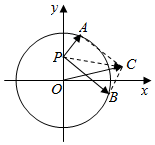 如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )
如图,已知点P(0,$\frac{\sqrt{2}}{3}$),点A,B是单位圆O上的两个动点,若$\overrightarrow{PA}$•$\overrightarrow{PB}$=0,动点C满足$\overrightarrow{PC}$=$\overrightarrow{PA}+\overrightarrow{PB}$,则关于|$\overrightarrow{OC}$|的说法正确的是( )| A. | |$\overrightarrow{OC}$|随点A,B位置的改变而变化,且最大值为$\frac{4}{3}$ | |
| B. | |$\overrightarrow{OC}$|随点A,B位置的改变而变化,且最小值为$\frac{4}{3}$ | |
| C. | |$\overrightarrow{OC}$|是一个常数,且值为$\frac{4}{3}$ | |
| D. | 以上说法都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com