
分析 化简得出g(θ)=$\frac{1}{2}$sin2θ+sin($θ+\frac{π}{3}$)$+\frac{\sqrt{3}}{4}$,判断不能同时达到最大值,只能够利用导数求解即可.
解答 解:∵g(θ)=$\frac{1}{2}$sin2θ+sin($θ+\frac{π}{3}$)$+\frac{\sqrt{3}}{4}$,
∴g′(θ)=cos2θ$+cos(θ+\frac{π}{3})$,
g′(θ)=0
即cos(2θ)=cos($θ+\frac{4π}{3}$),
∴2θ=$θ+\frac{4}{3}$π,2θ+θ$+\frac{4}{3}$π=2π
即θ=$\frac{4}{3}$π,$θ=\frac{2π}{9}$
∵θ∈(0,$\frac{π}{2}$),
∴$θ=\frac{2π}{9}$,
∴最大值为为:($\frac{1}{2}$+cos$\frac{2π}{9}$)($\frac{\sqrt{3}}{2}$+sin$\frac{2π}{9}$).
点评 本题考查两角和与差的正弦函数,涉及同角三角函数基本关系,属基础题


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
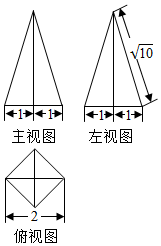 一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )
一个四棱锥的底面为正方形,其三视图如图所示,其中主视图和左视图均为等腰三角形,俯视图是一个正方形,则这个四棱锥的体积是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{a}$+$\overrightarrow{b}$ | B. | $\frac{1}{2}$$\overrightarrow{b}$+$\overrightarrow{a}$ | C. | $\frac{1}{2}$($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$+$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1-$\sqrt{2}$,0] | B. | [0,$\sqrt{2}$+1] | C. | [$\sqrt{2}$-1,$\sqrt{2}$+1] | D. | [1,$\sqrt{2}$+1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com