练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．两个不同的平面α、β，m为α内的一条直线，命题p：α⊥β，命题q：m⊥β，则p是q的（　　）
    A．充要条件B．充分不必要条件
    C．必要不充分条件D．既不充分也不必要条件

    分析 由命题q：m⊥β，m?α，可得α⊥β；反之不成立，m?β或m∥β或m与β相交．

    解答 解：由命题q：m⊥β，m?α，可得α⊥β；
    反之不成立，m?β或m∥β或m与β相交．
    因此p是q的必要不充分条件．
    故选：C．

    点评 本题考查了空间位置关系的判定、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    3．甲乙二人玩猜字游戏，先由甲在心中想好一个数字，记作a，然后再由乙猜甲刚才所想到的数字，并把乙猜到的数字记为b，二人约定：a、b∈{1，2，3，4}，且当|a-b|≤1时乙为胜方，否则甲为胜方．则甲取胜的概率是$\frac{3}{8}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．某种产品的广告费支出x（单位：百万元）与销售额y（单位：百万元）之间有如下对应数据：则回归直线方程必过（　　）
    x24568
    y3040605070
    A．（5，50）B．（5，60）C．（4，55）D．（4，50）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．已知函数f（x）=x2•sinx，各项均不相等的数列{xn}满足$|{x_i}|≤\frac{π}{2}（i=1，2，3，…n）$．令F（n）=（x1+x2+…+xn）•[f（x1）+f（x2）…+f（xn）]（n∈N*）．给出下列三个命题：
    ①存在不少于3项的数列{xn}，使得F（n）=0；
    ②若数列{xn}的通项公式为${x_n}={（-\frac{1}{2}）^n}$（n∈N*），则F（2k）＞0对k∈N*恒成立；
    ③若数列{xn}是等差数列，则存在n∈N*使得F（n）＜0成立
    其中真命题的序号是①②．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．某种产品广告的支出x与销售收入y（单位：万元）之间有下列所示的对应数据及统计数据．
    广告支出x/万元1234
    销售收入y/万元12284256
    $\overline{x}$$\overline{y}$$\sum_{i=1}^{4}$（$\overline{x}$i-$\overline{x}$）2$\sum_{i=1}^{4}$（$\overline{x}$i-$\overline{x}$）（yi-$\overline{y}$）
    $\frac{5}{2}$$\frac{69}{2}$573
    $\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$
    （1）画出表中数据的散点图；
    （2）求出y与x的回归直线方程；
    （3）若广告费为9万元，则销售收入约为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    18．已知两直线l1与l2的方向向量分别为$\overrightarrow{{v}_{1}}$=（1，-3，-2），$\overrightarrow{{v}_{2}}$=（-3，9，6），则l1与l2的位置关系为l1∥l2或重合．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

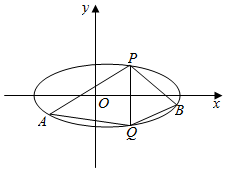    5．已知椭圆C的中心在原点，焦点在x轴上，离心率等于$\frac{{\sqrt{3}}}{2}$，它的两个顶点恰好是双曲线y2-x2=1的两个焦点．
    （1）求椭圆C的方程；
    （2）点P（2，1），Q（2，-1）在椭圆上，A，B是椭圆上位于直线PQ两侧的动点，满足于∠APQ=∠BPQ，试求直线AB的斜率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．执行如图所示的程序框图，若输入A的值为2.5，则输出的P值为（　　）
    A．6B．7C．8D．9

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．某种计算机病毒是通过电子邮件进行传播的，表格是某公司前5天监测到的数据：
    第x天12345
    被感染的计算机数量y（台）12244995190
    则下列函数模型中能较好地反映在第x天被感染的数量y与x之间的关系的是（　　）
    A．y=12xB．y=6x2-6x+12C．y=6•2xD．y=12log2x+12

    查看答案和解析>>

    同步练习册答案