
| 广告支出x/万元 | 1 | 2 | 3 | 4 |
| 销售收入y/万元 | 12 | 28 | 42 | 56 |
| $\overline{x}$ | $\overline{y}$ | $\sum_{i=1}^{4}$($\overline{x}$i-$\overline{x}$)2 | $\sum_{i=1}^{4}$($\overline{x}$i-$\overline{x}$)(yi-$\overline{y}$) |
| $\frac{5}{2}$ | $\frac{69}{2}$ | 5 | 73 |
分析 (I)根据所给的数据构造有序数对,在平面直角坐标系中画出散点图.
(II)观察散点图可知各点大致分布在一条直线附近,得到这组数据符合线性相关,求出利用最小二乘法所需要的数据,做出线性回归方程的系数,得到方程.
(III)把x=9代入线性回归方程,估计出当广告费为9万元时,销售收入约为129.4万元.
解答 解:(Ⅰ)作出的散点图如图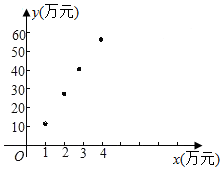
(Ⅱ)观察散点图可知各点大致分布在一条直线附近,列出下表:
| 序号 | x | y | x2 | xy |
| 1 | 1 | 12 | 1 | 12 |
| 2 | 2 | 28 | 4 | 56 |
| 3 | 3 | 42 | 9 | 126 |
| 4 | 4 | 56 | 16 | 224 |
| $\sum_{\;}^{\;}$ | 10 | 138 | 30 | 418 |
点评 本题考查了线性回归方程的求法,散点图的意义,利用线性回归方程进行数值估计,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
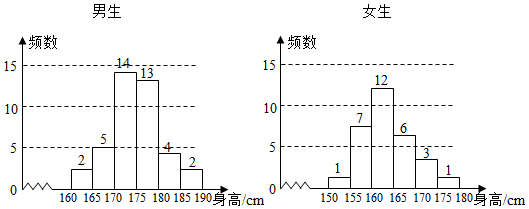
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | [4,+∞) | C. | [-4,4] | D. | (-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com