
| A. | (-∞,4] | B. | [4,+∞) | C. | [-4,4] | D. | (-4,4] |
分析 令t=x2-ax+3a,函数y=logsin1t是关于t的减函数,由此能求出实数a的取值范围.
解答 解:令t=x2-ax+3a,
∵sin1∈(0,1),
∴函数y=logsin1t是关于t的减函数,
结合题意,得t=x2-ax+3a是区间[2,+∞)上的增函数,
又∵在[2,+∞)上t>0总成立
∴$\left\{\begin{array}{l}{\frac{a}{2}≤2}\\{{2}^{2}-2a+3a>0}\end{array}\right.$,解之得-4<a≤4.
∴实数a的取值范围是(-4,4].
故选:D.
点评 本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意换元法和对数函数性质的合理运用.


科目:高中数学 来源: 题型:解答题
| 广告支出x/万元 | 1 | 2 | 3 | 4 |
| 销售收入y/万元 | 12 | 28 | 42 | 56 |
| $\overline{x}$ | $\overline{y}$ | $\sum_{i=1}^{4}$($\overline{x}$i-$\overline{x}$)2 | $\sum_{i=1}^{4}$($\overline{x}$i-$\overline{x}$)(yi-$\overline{y}$) |
| $\frac{5}{2}$ | $\frac{69}{2}$ | 5 | 73 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
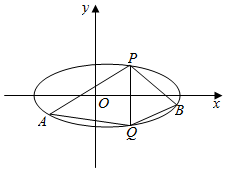 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,3) | B. | (-∞,1) | C. | (-1,+∞) | D. | (-3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [4$\sqrt{2}$,+∞) | B. | [3$\sqrt{2}$,+∞) | C. | [2$\sqrt{2}$,+∞) | D. | [$\frac{5}{2}$$\sqrt{2}$,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com