
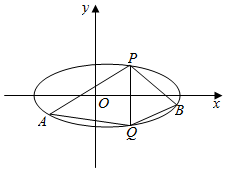
 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.分析 (1)由已知得椭圆的两个顶点坐标为$(0,\sqrt{2}),(0,-\sqrt{2})$,由此得到b2=2,由离心率为$\frac{{\sqrt{3}}}{2}$,得a2=8.由此能求出椭圆的方程.
(2)直线AP与直线BP的倾斜角互补,设A(x1,y1),B(x2,y2),kAP=k,则有kBP=-k,直线AP的方程y=k(x-2)+1,直线BP的方程y=-k(x-2)-1,由此分别把直线方程与椭圆方程联立,分别求出A、B的坐标,从而能求出直线AB的斜率.
解答 解:(1)∵椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{{\sqrt{3}}}{2}$,它的两个顶点恰好是双曲线y2-x2=1的两个焦点.
双曲线y2-x2=1的焦点为$(0,\sqrt{2}),(0,-\sqrt{2})$,
∴椭圆的两个顶点坐标为$(0,\sqrt{2}),(0,-\sqrt{2})$,
由于椭圆的焦点在x轴上,∴b2=2,由于离心率为$\frac{{\sqrt{3}}}{2}$,得a2=8.
由此可得椭圆的方程为$\frac{x^2}{8}+\frac{y^2}{2}=1$.
(2)∵∠APQ=∠BPQ,∴直线AP与直线BP的倾斜角互补,
设A(x1,y1),B(x2,y2),kAP=k,则有kBP=-k,
直线AP的方程y=k(x-2)+1,直线BP的方程y=-k(x-2)-1,
联立方程$\left\{{\begin{array}{l}{\frac{x^2}{8}+\frac{y^2}{2}=1}\\{y=k(x-2)+1}\end{array}}\right.$,化简得(1+4k2)x2+(8k-16k2)x+16k2-16k-4=0,
由于直线AP与椭圆的交点为A、P,∴$2{x_1}=\frac{{16{k^2}-16k-4}}{{1+4{k^2}}}$,
即${x_1}=\frac{{8{k^2}-8k-2}}{{1+4{k^2}}}$,代入直线方程AP得:${y_1}=\frac{{-4{k^2}-4k+1}}{{1+4{k^2}}}$,
A点的坐标为$(\frac{{8{k^2}-8k-2}}{{1+4{k^2}}},\frac{{-4{k^2}-4k+1}}{{1+4{k^2}}})$,
∴B点的坐标为$(\frac{{8{k^2}+8k-2}}{{1+4{k^2}}},\frac{{-4{k^2}+4k+1}}{{1+4{k^2}}})$,
∴${k_{AB}}=\frac{1}{2}$.
点评 本题考查椭圆方程的求法,考查直线的斜率的求法,是中档题,解题时要认真审题,注意双曲线、椭圆、韦达定理、斜率公式等知识点的合理运用.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 只有一条,不在平面α内 | B. | 只有一条,且在平面α内 | ||
| C. | 有无数条,一定在平面α内 | D. | 有无数条,不一定在平面α内 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4] | B. | [4,+∞) | C. | [-4,4] | D. | (-4,4] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,8) | B. | (-∞,-2)∪(8,+∞) | C. | (-4,16) | D. | (-∞,-4)∪(16,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com