
分析 作出M在准线上的射影,根据|KM|:|MN|确定|KN|:|KM|的值,进而列方程求得a.
解答 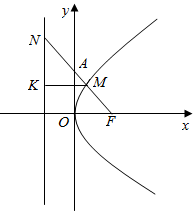 解:依题意F点的坐标为( $\frac{a}{4}$,0),
解:依题意F点的坐标为( $\frac{a}{4}$,0),
设M在准线上的射影为K,由抛物线的定义知|MF|=|MK|,
∴|KM|:|MN|=1:5,
则|KN|:|KM|=2$\sqrt{6}$:1,
∵kFN=$\frac{0-2}{\frac{a}{4}-0}$=-$\frac{8}{a}$,kFN=-2$\sqrt{6}$
∴$\frac{8}{a}$=2$\sqrt{6}$,求得a=$\frac{{2\sqrt{6}}}{3}$.
故答案为:$\frac{{2\sqrt{6}}}{3}$.
点评 本题主要考查了抛物线的简单性质.抛物线中涉及焦半径的问题常利用抛物线的定义转化为点到准线的距离来解决.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{8}{25}$ | B. | $\frac{8}{5}$ | C. | $\frac{8}{25}$ | D. | $\frac{{1-2\sqrt{6}}}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=2x | B. | y2=3x | C. | y2=4x | D. | y2=x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方体ABCD-A1B1C1D1中,点M,N分别是CD、DD1的中点.
如图,正方体ABCD-A1B1C1D1中,点M,N分别是CD、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com